Locked Candidate Type 1 and 2 Sudoku Technique + Examples

The locked candidate Sudoku technique can help you eliminate candidates or find answers to cells by looking for a candidate in one unit (row, column, or block) that overlaps a second unit, thus locking that candidate into place at the intersection of both units.

You can use this Sudoku strategy to eliminate candidates in a variety of Sudoku puzzles, from intermediate to hard, so you can find answers faster and solve puzzles easier.

How to Find Locked Candidates

If you're familiar with naked pairs, you'll recognize how locked candidates also restrict candidate positions - but across units.

To find locked candidates, use pencil marks to note all the candidates in a puzzle. Then look for instances where a single candidate can only appear in one row, column, or block within another unit. For example, if candidate 9 only appears in row 3 (H3 and I3) in the rightmost 3x3 block and nowhere else in that block, then 9 must be the answer to one of those cells.

Where the units overlap creates a restriction that limits where that candidate can go in the other unit, row 3, allowing you to eliminate it from other cells in that unit outside of the overlap. In this case, if 9 were an answer to B3 or E3, the rightmost block wouldn't have a 9. Because the 9s are locked in row 3, block 3, you can eliminate 9 as a candidate from the rest of row 3 outside that block, specifically B3 and E3.

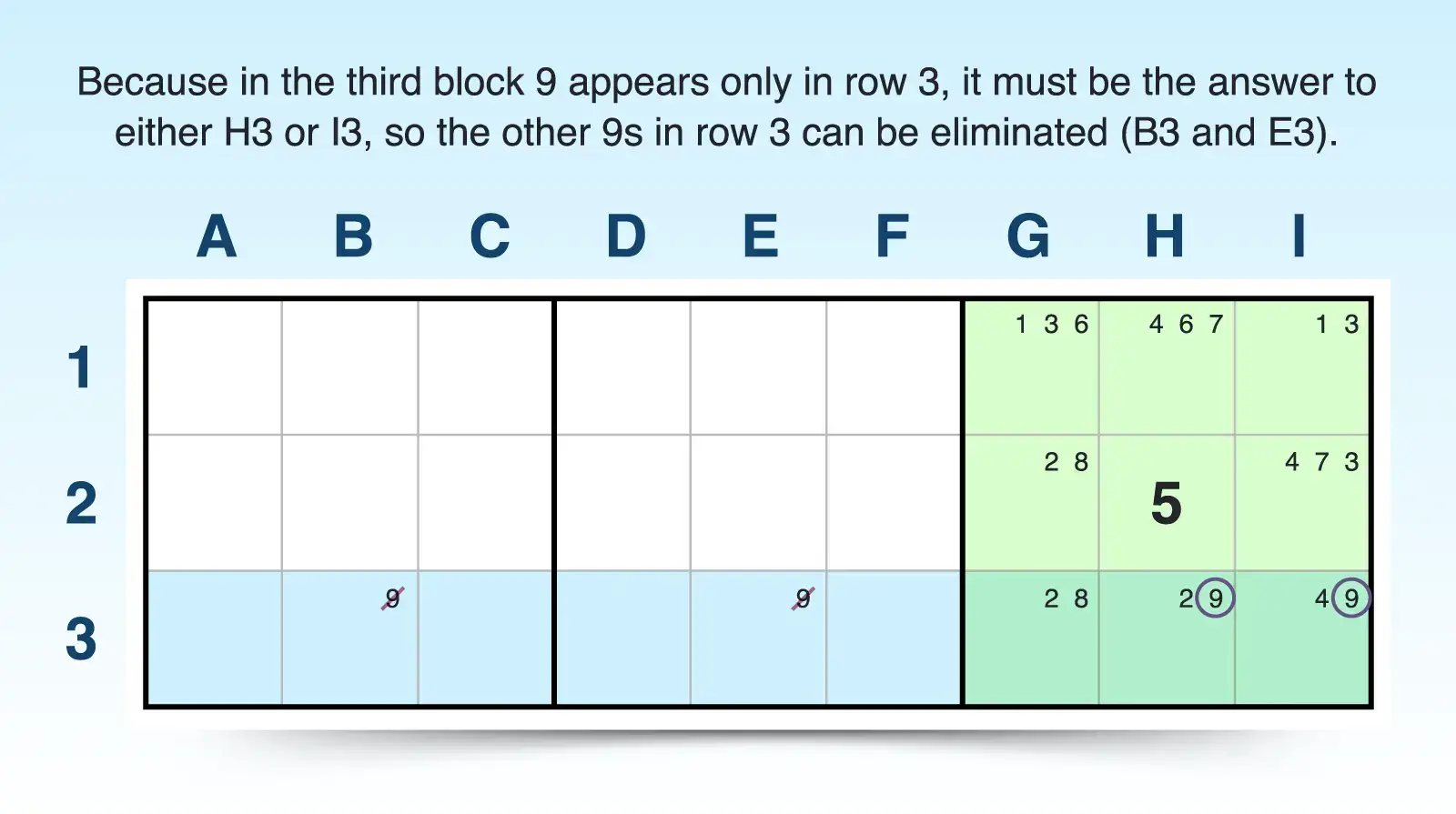
Locked Candidate Examples

Sudoku solvers often refer to two types of locked candidates: pointing (or block-line elimination) and claiming (line-block elimination), referring to the logic used in each strategy.

• A pointing locked candidate points to eliminations in a single row or column outside of a block.
• A claiming locked candidate claims the candidate within the block in a single row or column, thus eliminating the candidate from other cells within the block.

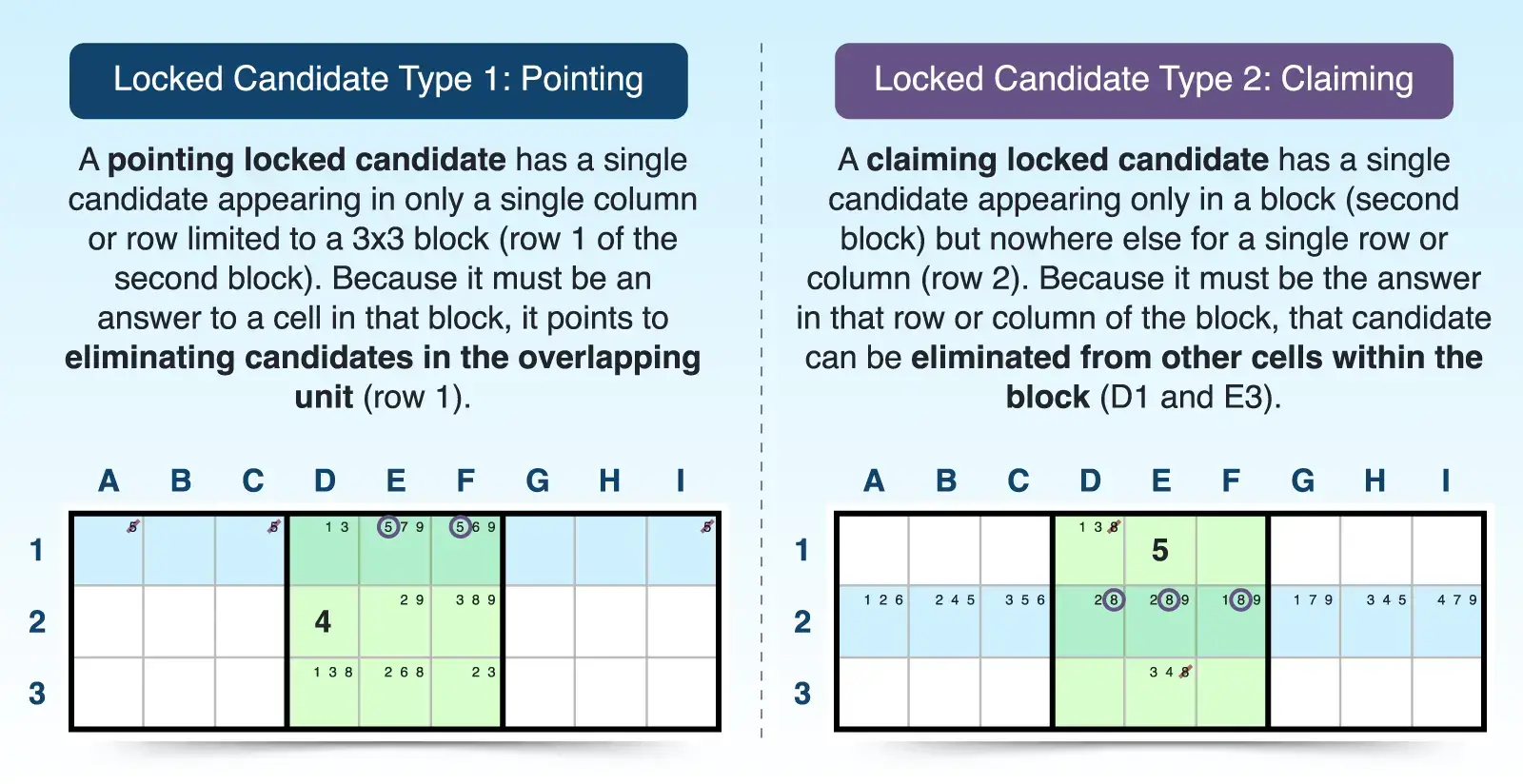
Locked Candidates Type 1: Pointing

The pointing locked candidate strategy uses a 3x3 block to eliminate candidates from a row or column outside of that block. The technique works like this:

• If: A single candidate appears only within one row or column in a 3x3 block, it must be the answer to one of the cells within that block.
• Then: You can eliminate that candidate from the rest of the row or column outside of the block.

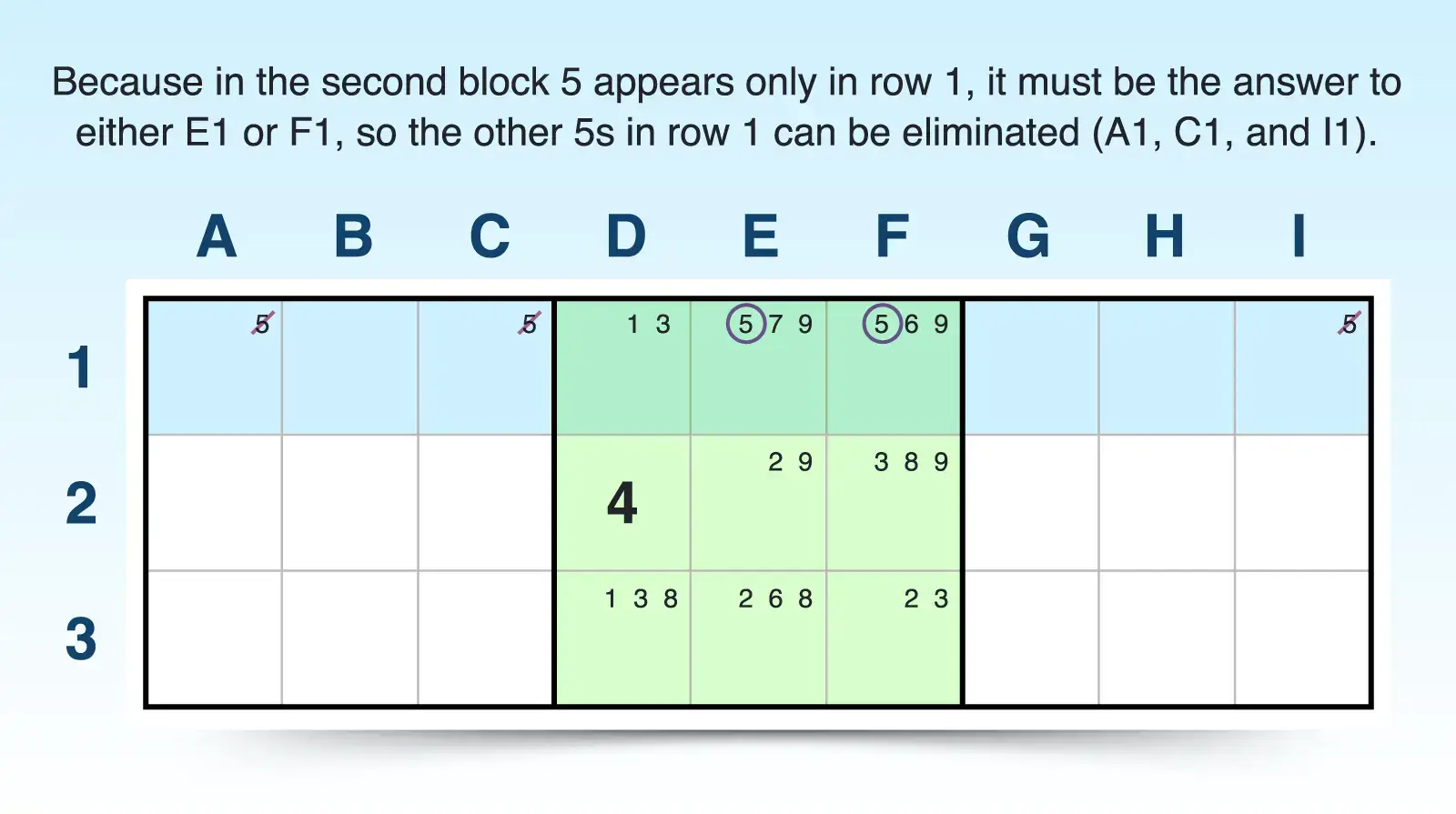
For example, if you have a 5 candidate that appears only in row 1 in the second block and nowhere else in that block, then 5 must be an answer in either E1 or F1 of that block. That means 5 can't be an answer anywhere else in row 1 and can be eliminated from A1, C1, and I1.

The elimination can occur because if 5 appeared elsewhere in row 1 outside the second block, then it couldn't be placed in that block at all, violating the rule that every block must contain each number exactly once.

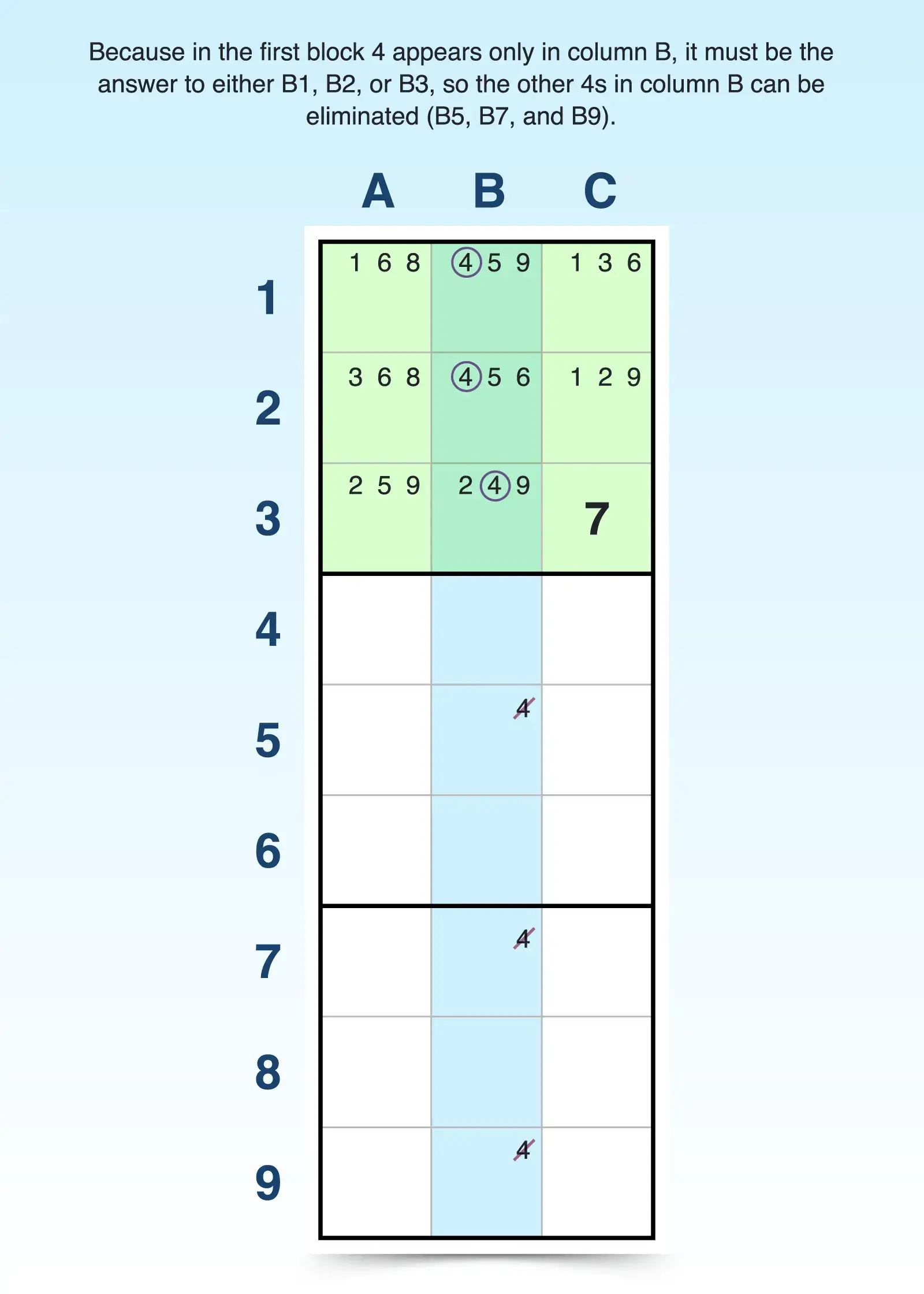
The same can happen with a column. If candidate 4 appears only in column B within the first 3x3 block, then it can't be a candidate anywhere else in column B. You can eliminate it from cells in that column outside of the block (B5, B7, and B9) because B1, B2, or B3 must have a 4 in it.

Locked Candidates Type 2: Claiming

The claiming locked candidate strategy uses a row or column to eliminate a specific digit from within a block. This Sudoku solving technique works like this:

• If: A candidate appears only within one 3x3 block and nowhere else for a single row or column, that candidate must be an answer in that block for that particular row or column.
• Then: You can eliminate that candidate from other cells within that block that are not in that row or column.

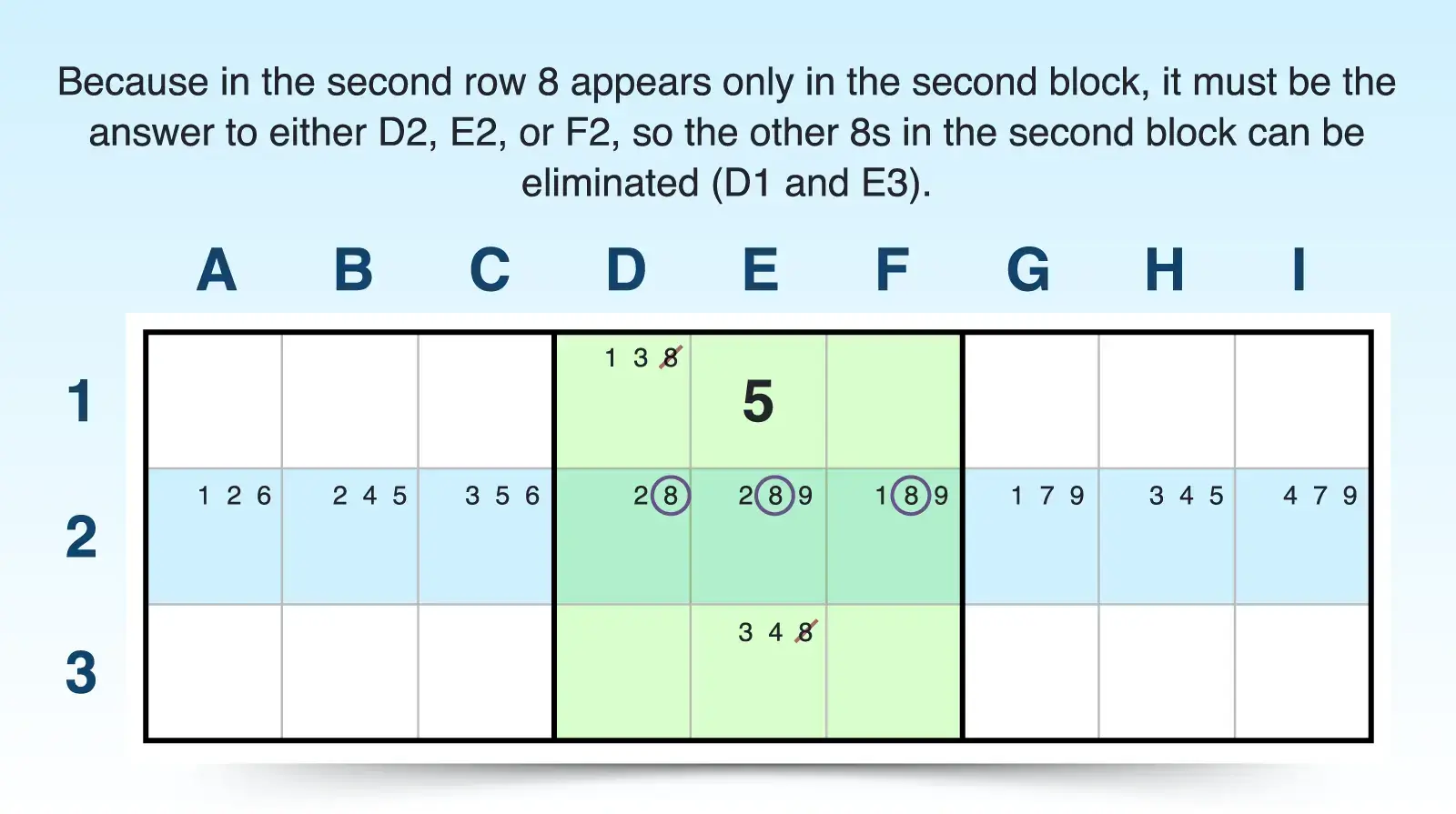
For example, if candidate 8 only appears in the second block in row 2 and nowhere else in that row, it must be the answer to one of those cells (D2, E2, or F2). So 8 cannot be an answer elsewhere in the block. If D1 was an 8, then row 2 would not have an 8 in it. That means you can eliminate 8 as a candidate from any other cells within the second block except those in row 2, which would be D1 and E3.

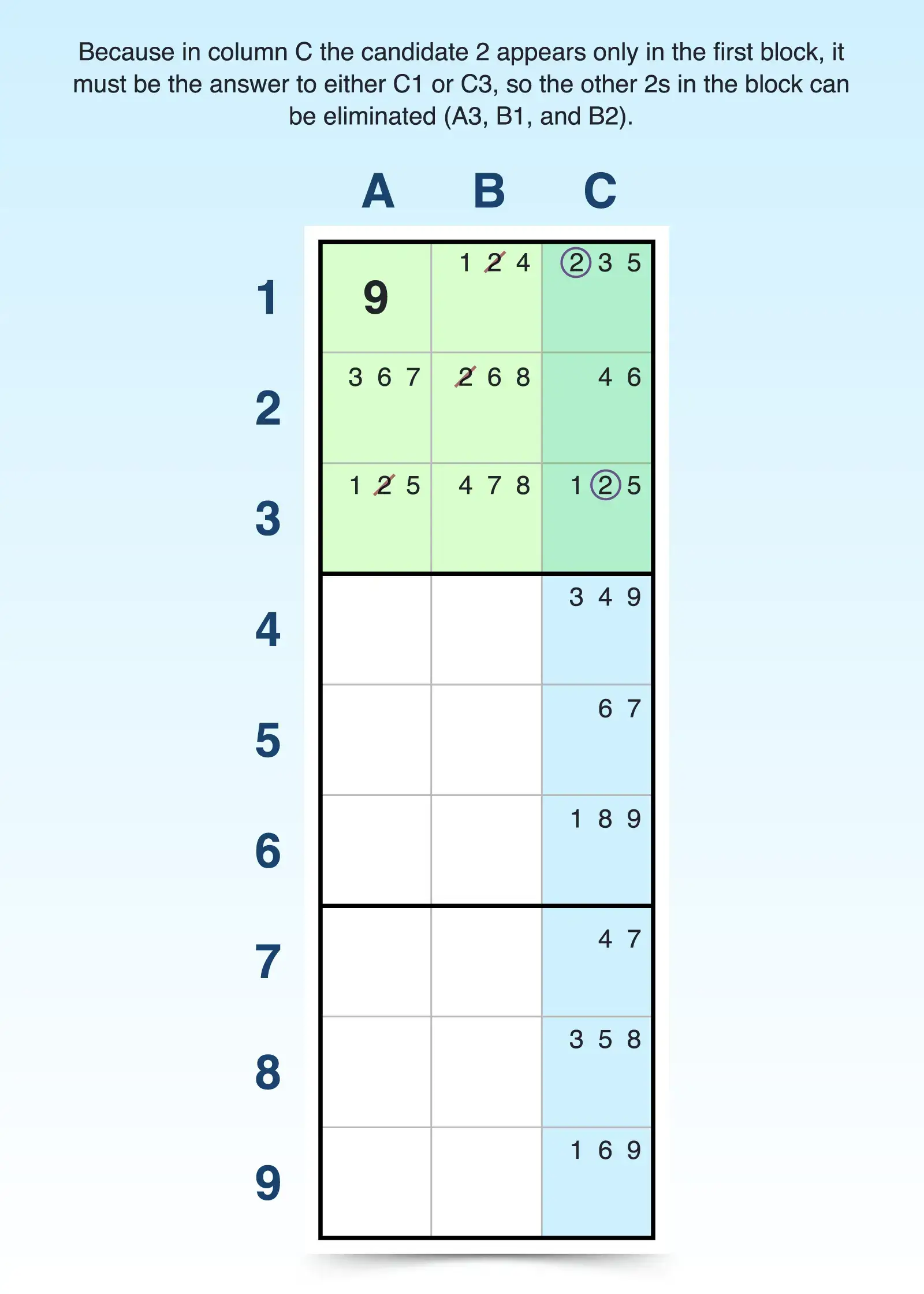
The same can be true of a column. If candidate 2 appears only in the first block in column C and nowhere else in that column, then it must be the answer for one of those cells (C1 or C3). That means 2 cannot be an answer anywhere else in that block. If A3 was a 2, then column C would have no 2 in it. So you can eliminate 2 from other cells within the first block except for those in column C (A3, B1, and B2).

The locked candidate strategy can help you eliminate candidates when you play Sudoku online. So level up your skills and practice this technique on our expert puzzles or explore our archive for even more puzzles to solve.