Forcing Chains Sudoku Technique + Examples

Although forcing chains is an advanced strategy for solving Sudoku puzzles, you can easily use this technique once you understand the simple logic behind it. Similar to Sudoku coloring, the forcing chains Sudoku technique simply means you start with a cell and create a chain of what-if scenarios, to force the truth or falsity of an answer.

A type of alternating inference chain (AIC), forcing chains means you pretend that each candidate in a starting cell is the answer for that cell, and then you follow the chain reaction of answers you create for each candidate. From cell-forcing chains to digit-forcing chains, this logical form of trial and error—not guesswork—helps you confirm or eliminate candidates.

Forcing chains is not a difficult Sudoku strategy to use, but the logic can get complex when the chains grow long and involve multiple what-if scenarios. Still, sticking with the logic can help you level up your skills and solve hard and expert Sudoku puzzles even faster.

Possible Outcomes of Forcing Chains

Forcing chains is not a pattern you spot. Instead, you use logical conclusions to confirm or eliminate candidates. Once you’ve identified a cell to begin the forcing chains technique with, take turns assuming that each candidate in that cell is the answer. Then follow the chain of what-ifs to another cell. Using forcing chains can lead to many different outcomes:

• If the choices in the first cell come to the same conclusion for the last cell in the chain, then you’ve proven that the conclusion must be true for the last cell. So, if the last cell’s answer is 3 regardless of which candidate you began with, then you confirm that the answer for that last cell is 3 and can eliminate other candidates from the cell.
• If the paths come to different conclusions within the same last cell, then you can narrow down candidates in the last cell because you’ve proven that the last cell must be one of those candidates. If each candidate you began with offered a different answer for the last cell, then you know those answers are the only possible candidates for that cell. You can eliminate any additional candidates from the cell.
• If the choices result in a contradiction, then you know the candidate you began with must be eliminated as it leads to a breakdown in logic.

How to Use the Forcing Chains Sudoku Technique

To find a useful opportunity for using the forcing chains solving technique, you need to use pencil marks throughout the puzzle to mark all possible candidates, and you should exhaust all other strategies.

In its simplest form, you start with one bi-value cell (a cell that has just two candidates), but you can use cells with more than two candidates—it just makes following the logic a bit more complicated.

Regardless of how many candidates a cell has, follow these steps, using a bi-value cell as an example, to force conclusions or find eliminations:

1. Look for a starting cell. Find a cell that seems to have potential for creating a chain reaction of answers. A bi-value cell with just two candidates is the simplest form because you know that one of those two digits must be the answer to that cell. For example, C1 has just two candidates (5, 8).


2. Make conclusions based on one of the digits in the cell. To begin you’re going to make the initial assumption that a single digit is the answer and see how that impacts others cells in the puzzle. It can be helpful to keep the chain noted on a separate piece of paper or in a table or spreadsheet.
   
   For example, if 5 is the answer for C1, then C4 has to be a 1. If C4 is a 1, then A4 has to be a 6. If A4 is a 6, then A9 has to be a 4. If A9 is a 4, then A3 has to be a 9, and the chain ends.



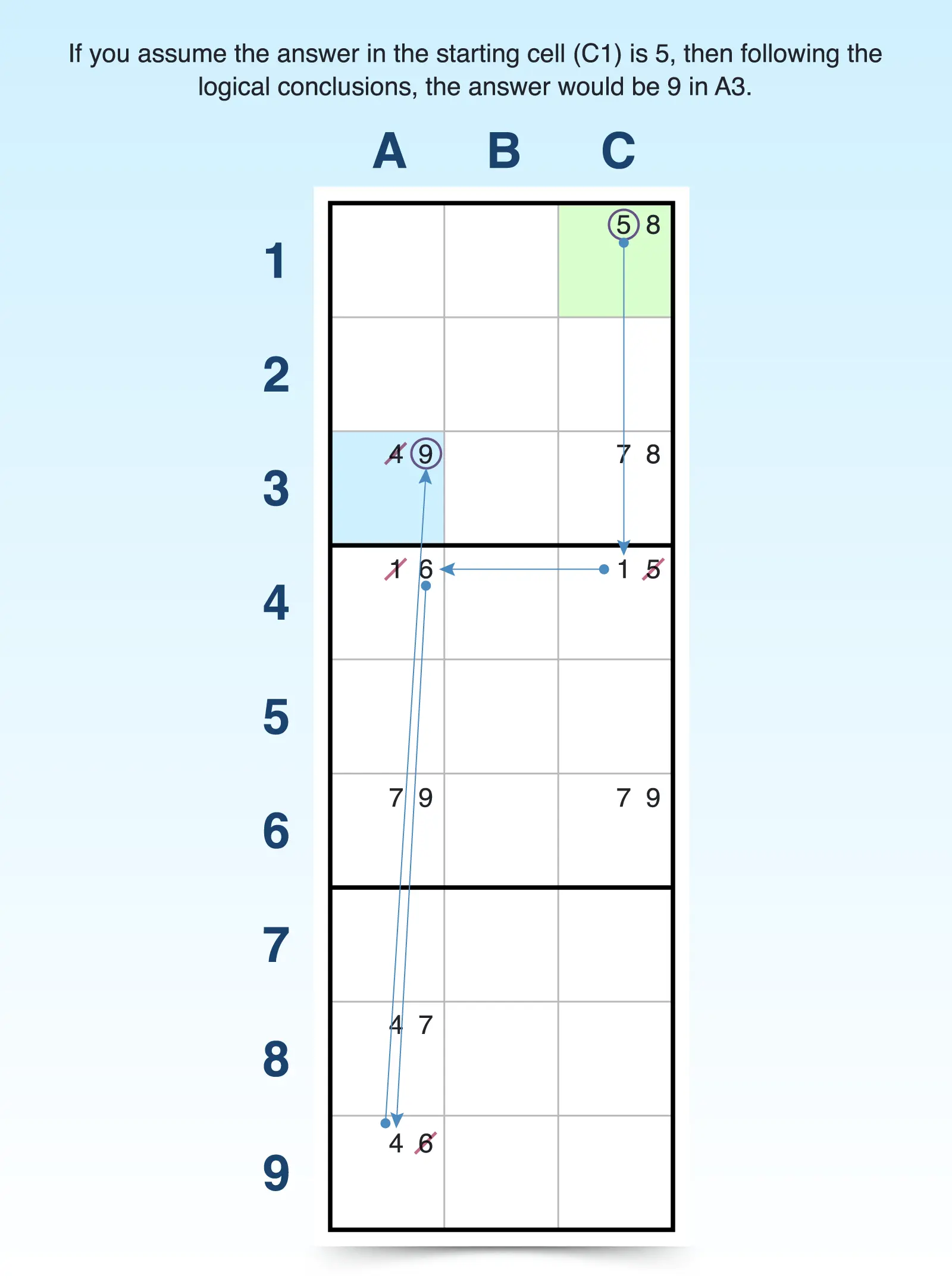
3. Make conclusions based on the other digits in the cell. Now that you know how the answer turns out based on one digit, your goal is to repeat the process with the other digits in the cell to see if you get the same answer or something different. You won’t follow the same path and may have a shorter or longer chain.
   
   For example, the bi-value cell has just one more candidate to use. If 8 is the answer to C1, then 7 must be the answer to C3. If 7 is the answer to C3, then 9 must be the answer to C6. If 9 is the answer to C6, then 7 must be the answer to A6. If 7 is the answer to A6, then 4 must be the answer to A8. If 4 is the answer to A8, then 9 must be the answer to A3.



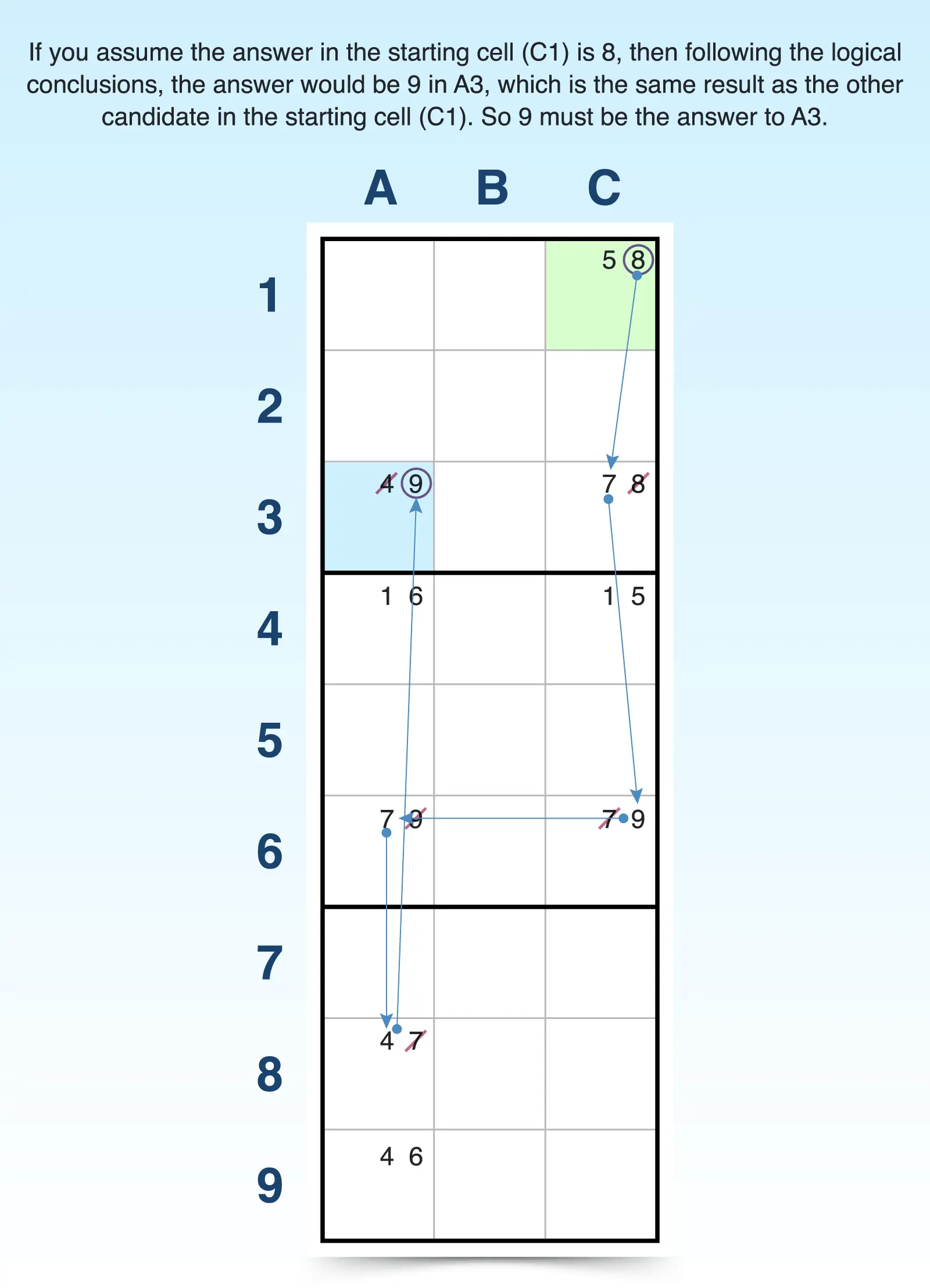
4. Confirm or eliminate candidates. If all candidates in the starting cell come to the same conclusion in the last cell, then that conclusion must be true. For example, both candidates found 9 to be the answer in A3. This is a simple example that offers just one possible result for forcing chains. Our examples in the next section can show you even more possibilities.

Forcing Chains Sudoku Technique Examples

Because forcing chains is not a pattern and because you have several different chains that can occur in a puzzle, you must remember that the conclusion is what drives your action. Following the logical answers and noting the overall conclusion helps you eliminate or confirm candidates in a Sudoku puzzle.

Forcing Chains: Same Result

The initial example showed how a bi-value starting cell resulted in the same answer no matter what candidate you began with. However, the “same result” doesn’t always mean you’re confirming an answer. A forcing chain could also eliminate a candidate if all assumptions come to the same conclusion—that a candidate cannot be an answer in the last cell.

Follow these steps to understand what to do if a forcing change comes to the same result for an elimination:

1. Look for a starting cell. Using a bi-value cell with just two candidates is a quick way to get started, but you can use any cell in the puzzle. For example, B2 has just two candidates (3, 9).


2. Make conclusions based on one of the digits in the cell. Begin with the first possible candidate and consider what chain reactions would result if that candidate was the answer to that cell.
   
   For example, if the answer to B2 is 3, then the answer to C3 has to be 5. If the answer to C3 is 5, then the answer to C9 has to be 9. If the answer to C9 is 9, then the answer to I9 has to be 8. If the answer to I9 is 8, then the answer to I4 has to be 2. If the answer to I4 is 2, then the answer to E4 has to be 1. If the answer to E4 is 1, then 1 cannot be the answer to D4 because it shares the same 3x3 block as E4.



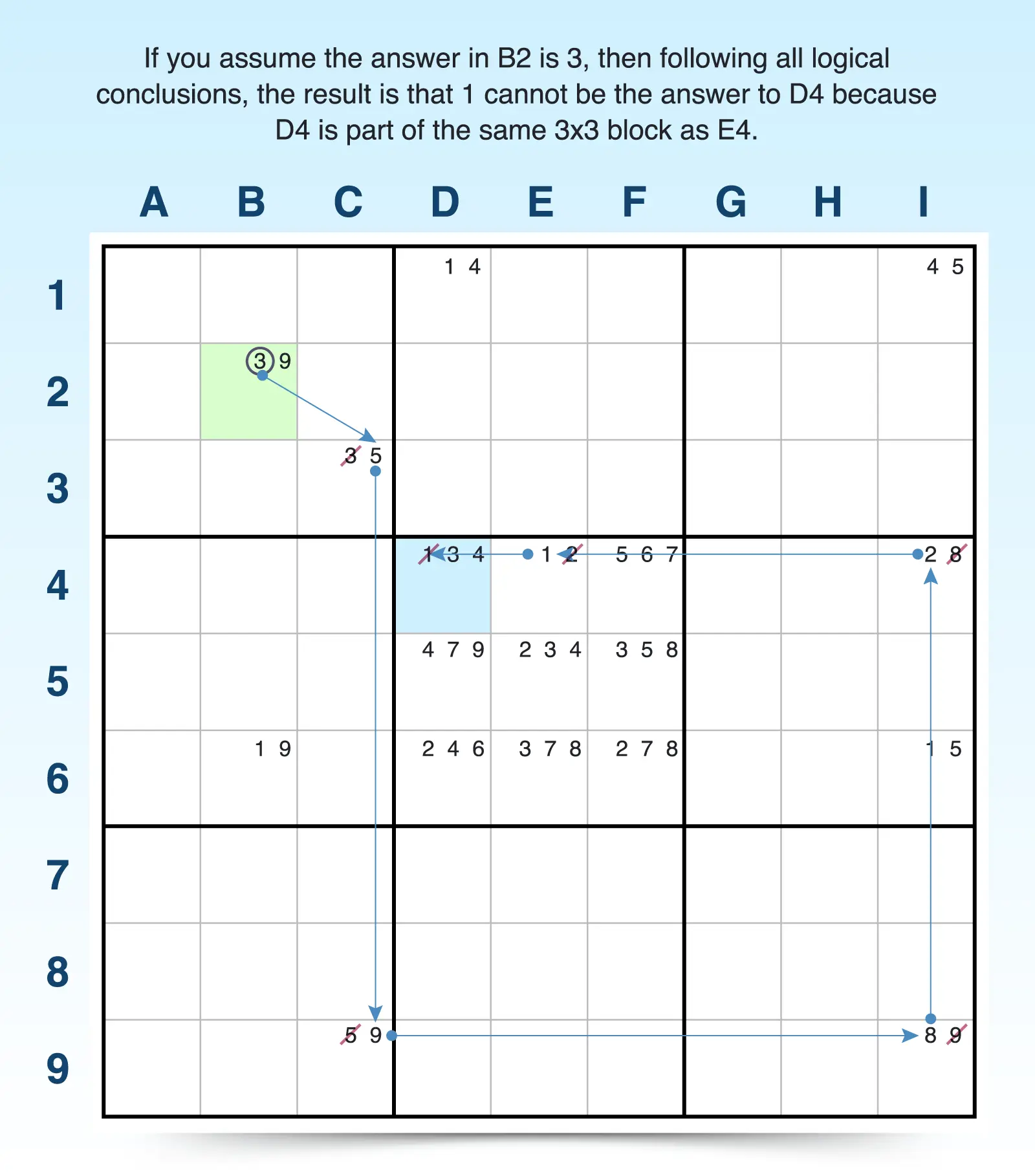
3. Make conclusions based on the other digits in the cell. You can now use the other digit in the starting cell and assume it is the answer. Then see the conclusions from that chain reaction.
   
   For example, if B2 is 9, then B6 must be 1. If B6 is 1, then I6 must be 5. If I6 is 5, then I1 must be 4. If I1 is 4, then D1 must be 1. If D1 is 1, then D4 cannot be 1.



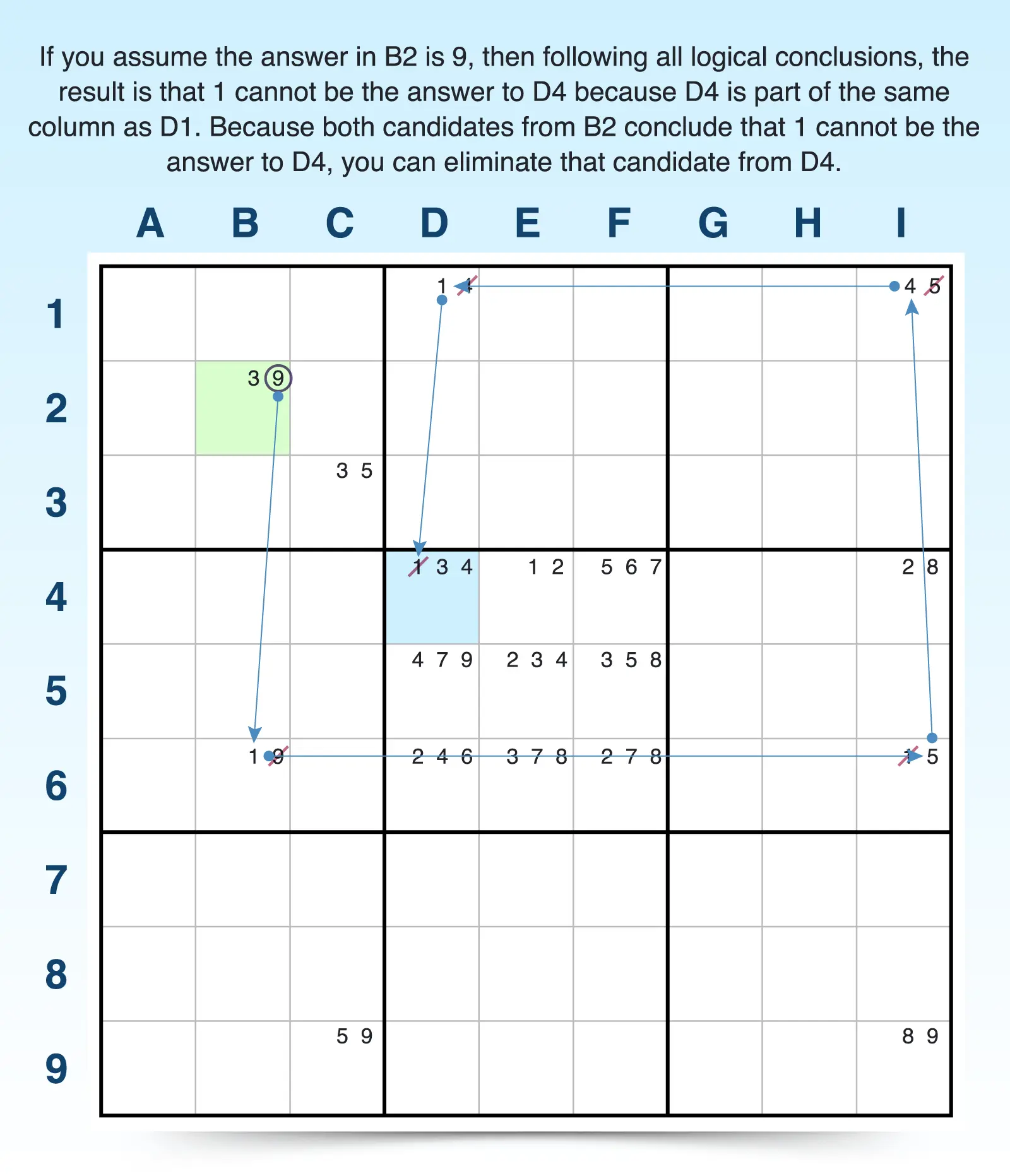
4. Confirm or eliminate candidates. Check to see if all candidates in the starting cell come to the same conclusion. If that’s the case, then that conclusion must be true. For example, both candidates in B2 concluded that 1 cannot be the candidate in D4. Because they both came to the conclusion, it must be true, and 1 can be eliminated from D4.

Forcing Chains: Different Results

If you use the forcing chains Sudoku technique, you could discover that all your starting assumptions lead to different results. If this happens, the likely conclusion is that all confirmed candidates are the only possible candidates in a cell.

Follow these steps to understand what to do when your forcing chain returns differing results:

1. Look for a starting cell. Select a cell you think will help create a lot of chain reactions in the puzzle. For example, E7 has just two candidates (1, 5) and makes an easy starting point.


2. Make conclusions based on one of the digits in the cell. Anytime you use forcing chains, you make an assumption that one of the digits is the answer for that cell and consider the conclusions that follow.
   
   For example, if you assume that the answer to E7 is 1, then B7 must be 3. If B7 is 3, then C9 must be 8. If C9 is 8, then C2 must be 7. If C2 is 7, then H2 must be 6.



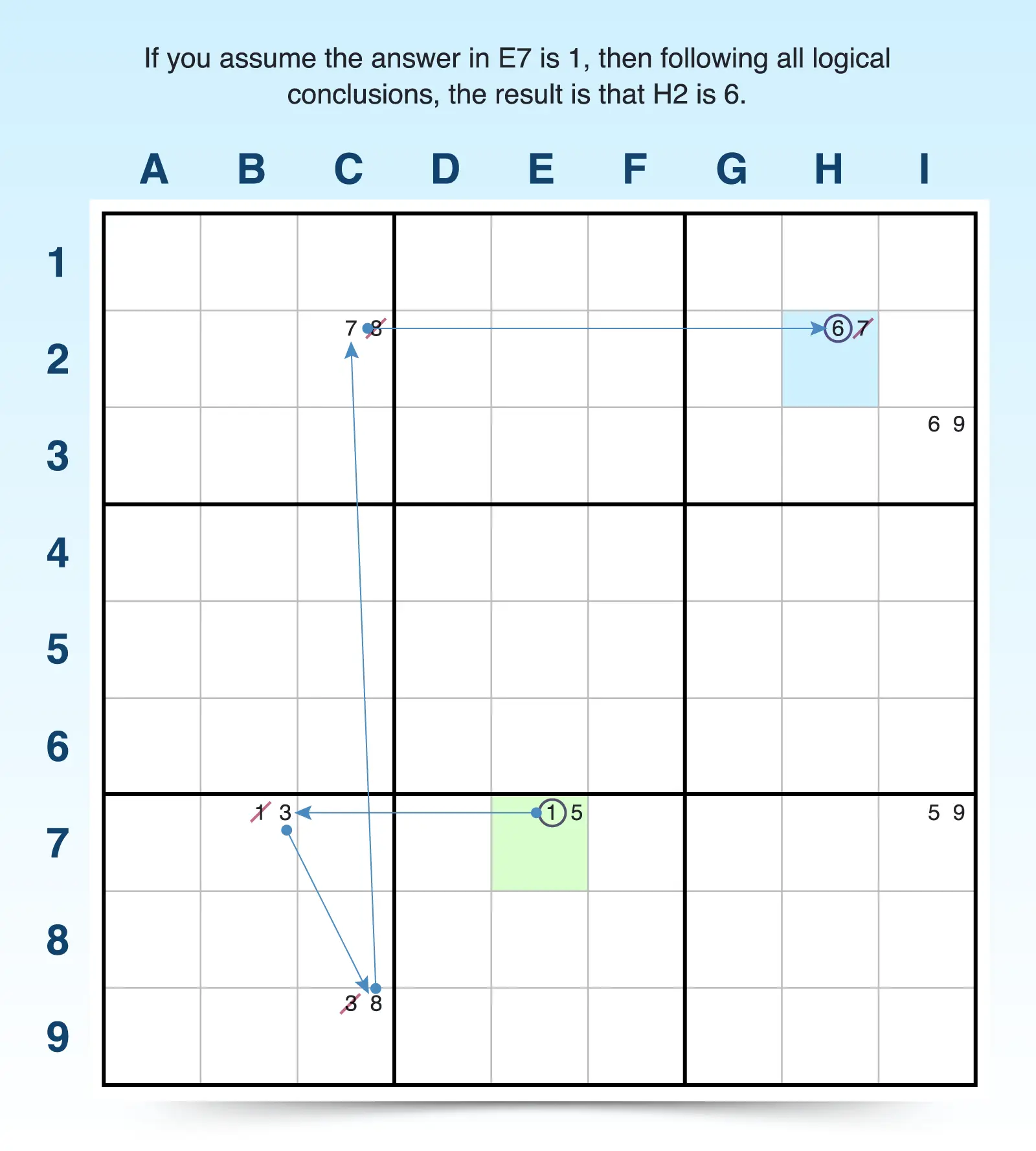
3. Make conclusions based on the other digits in the cell. You must repeat the process with all remaining digits—assume each remaining digit is the answer and then consider the result.
   
   For example, if the answer to E7 is a 5, then I7 must be 9. If I7 is 9, then I3 must be 6. If I3 is 6, then H2 must be 7 because it shares the same 3x3 block with I3.



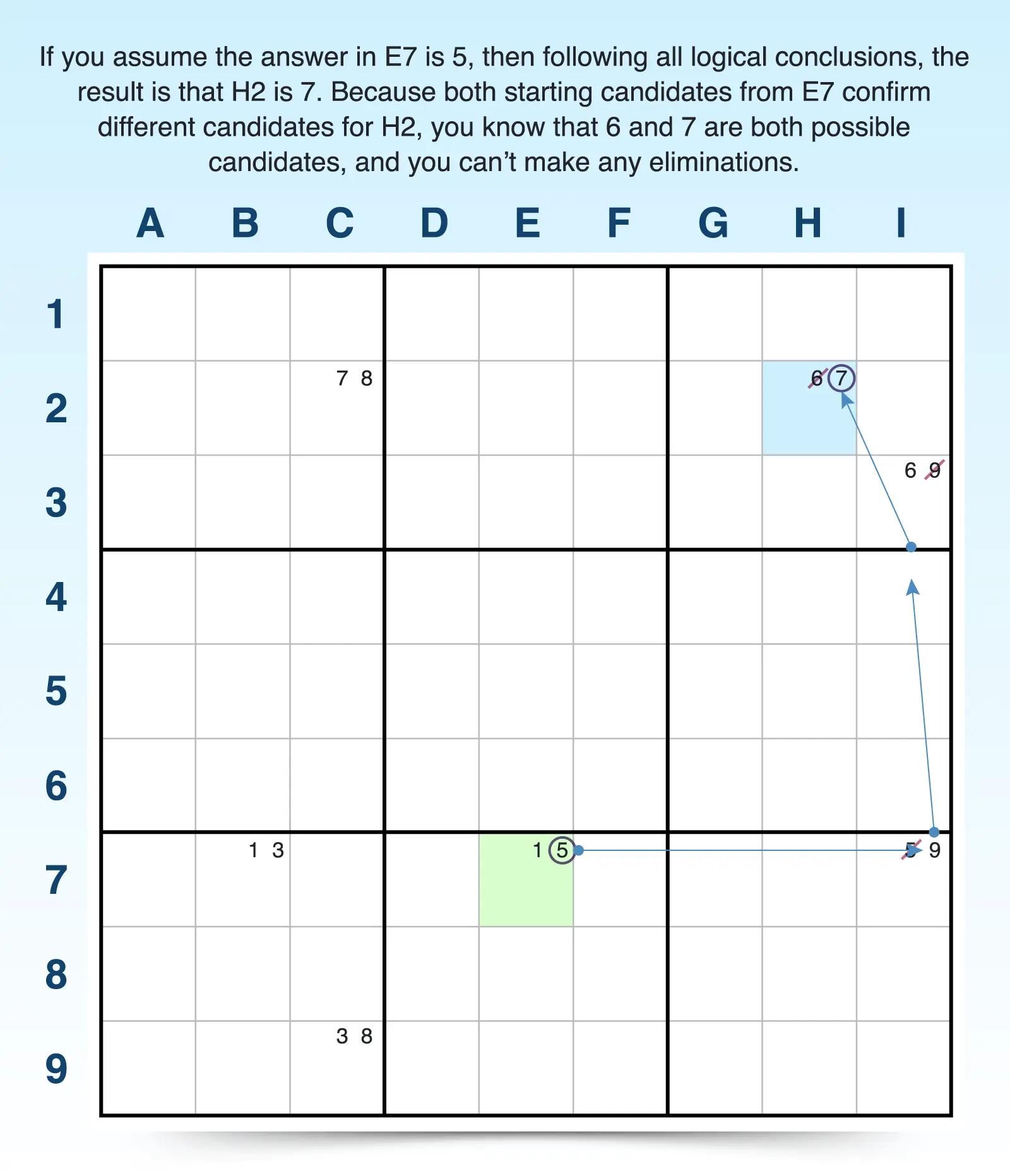
4. Confirm or eliminate candidates. If both candidates in the starting cell come to different conclusions in the last cell, then you know that both conclusions could possibly be true. In example, each candidate in E7 led to a different answer in H2. So you can be sure that 6 and 7 are both possible candidates for that cell and none can be eliminated.

Forcing Chains: Contradiction in Logic

Another outcome from forcing chains could be that your answer at the end of the chain causes a contradiction in logic and breaks the logic of the puzzle. If you cause a contradiction, then that means the candidate you used from the starting cell as the answer could not be the answer for that cell, and it can be eliminated.

In the example below, the contradiction occurs when a chain forces a 2 into a block that already contains a 2 answer in I9. While this candidate could be eliminated simply by noticing the conflict with the answer, tracing the contradiction through a chain highlights how forcing logic works and helps confirm eliminations that might otherwise go unnoticed.

Follow these steps:

1. Look for a starting cell. Like any forcing chain, you look for a cell with a good possibility for creating a chain reaction of answers. For example, B3 has just two candidates (4, 6).


2. Make conclusions based on one of the digits in the cell. Begin by assuming that one candidate is the answer to the cell. For example, if 4 is the answer for B3, then C1 has to be 5. If C1 is 5, then C7 has to be 1. If C7 is 1, then G7 has to be 2. But it can’t be 2 because it shares a 3x3 block with I9, which already has a 2 in it.



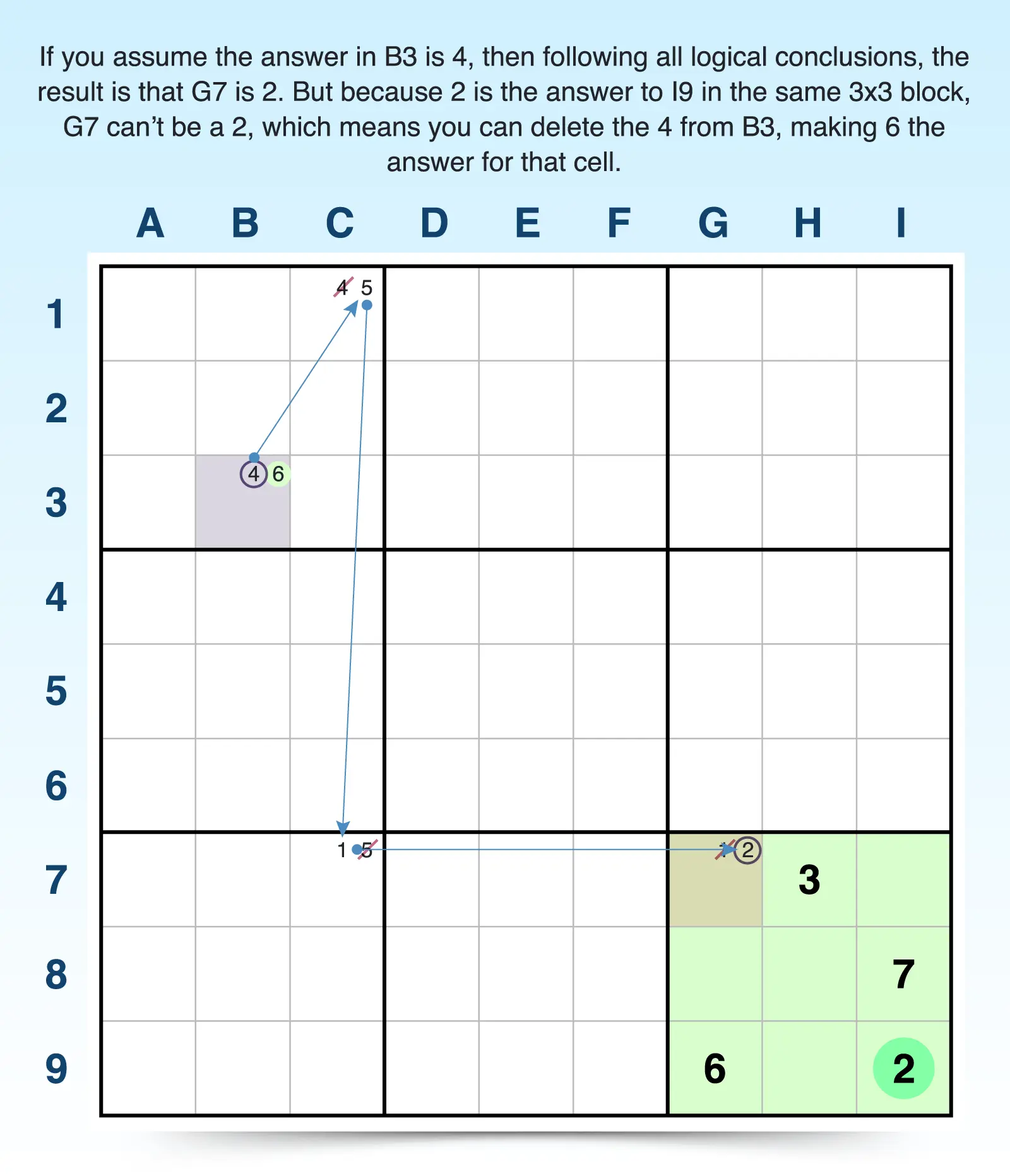
3. Confirm or eliminate candidates. If the conclusion reached creates a contradiction in logic, then you know you can delete the candidate you began with. For example, B3 can’t be 4 because it results in a 3x3 block having two 2s, which breaks the logic in the Sudoku puzzle. So you can delete 4 from B3, leaving 6 as the answer.

When you play Sudoku online and get stuck after using several advanced strategies, you can utilize forcing chains to help eliminate more candidates or confirm answers in your puzzles. Because most solvers use the Sudoku solving technique after advanced methods are exhausted, you should practice forcing chains on our hard Sudoku puzzles and get even more practice by exploring our archive.