X-Cycle Sudoku Strategy + Examples

X-cycles are powerful logic patterns that help eliminate candidates in Sudoku puzzles. A type of alternating inference chain (AIC), they use alternating strong and weak links between cells for a single digit, forming closed loops or chains of logical inference. When you find a properly alternating X-cycle for a single candidate, you can eliminate that candidate from off-chain cells (cells outside the chain) that see both ends of either a strong or weak link.

While X-cycles may seem advanced at first, they follow consistent rules and can lead to clean eliminations without guessing. Once you learn how to spot them, they can become a reliable part of your solving toolkit, especially in hard Sudoku puzzles.

How to Find X-Cycles

Suitable for more difficult puzzles, the X-cycle strategy is similar to Sudoku simple coloring and relies on finding a single-digit loop composed of alternating strong and weak links. When formed correctly, these logical chains allow you to eliminate candidates by following the consequences of each link.

While X-cycles are part of a broader family of Sudoku techniques known as Nice Loops, they are a specific, more constrained subset, making them easier to spot and apply consistently in more difficult puzzles.

Understand Strong and Weak Links

You’ll come across a lot of “loop” language that overlaps with X-cycles, which can be confusing. Loops and X-cycles are just different types of alternating inference chains (AIC) that rely on using strong and weak links to create loops or patterns.

• A strong link most commonly exists when the same candidate appears in exactly two cells within a unit (row, column, or box). So the link created between the two candidates results in: If one is false, the other must be true. The link is strong because it forces a truth (verity), and it works both directions for either candidate in either cell. For example, if the naked pair (3, 8) appears only twice in a row, column, or block, it results in a strong link between the two 3s and a strong link between the two 8s because if one 3 is not the answer, the other has to be the answer. The same holds true for candidate 8.
• A weak link is most easily recognized when the same candidate appears in more than two cells in a unit. The link between the multiple candidates results in: If one is true, the other must be false, but not vice versa. The link is weak because it’s not forcing a verity or confirming an answer, and it can’t work the other direction (prove something to be true) because of the multiple candidates. For example, if 8 is a candidate in three cells in a block, if one of the 8s is the answer, the others must be false. However, if one of the 8s is not the answer, you can’t confirm it as the answer in another cell in the block because you have two other 8s in that block.

Ensure the X-Cycle Follows These Rules

X-cycles are unique from other AICs because they must meet the following criteria:

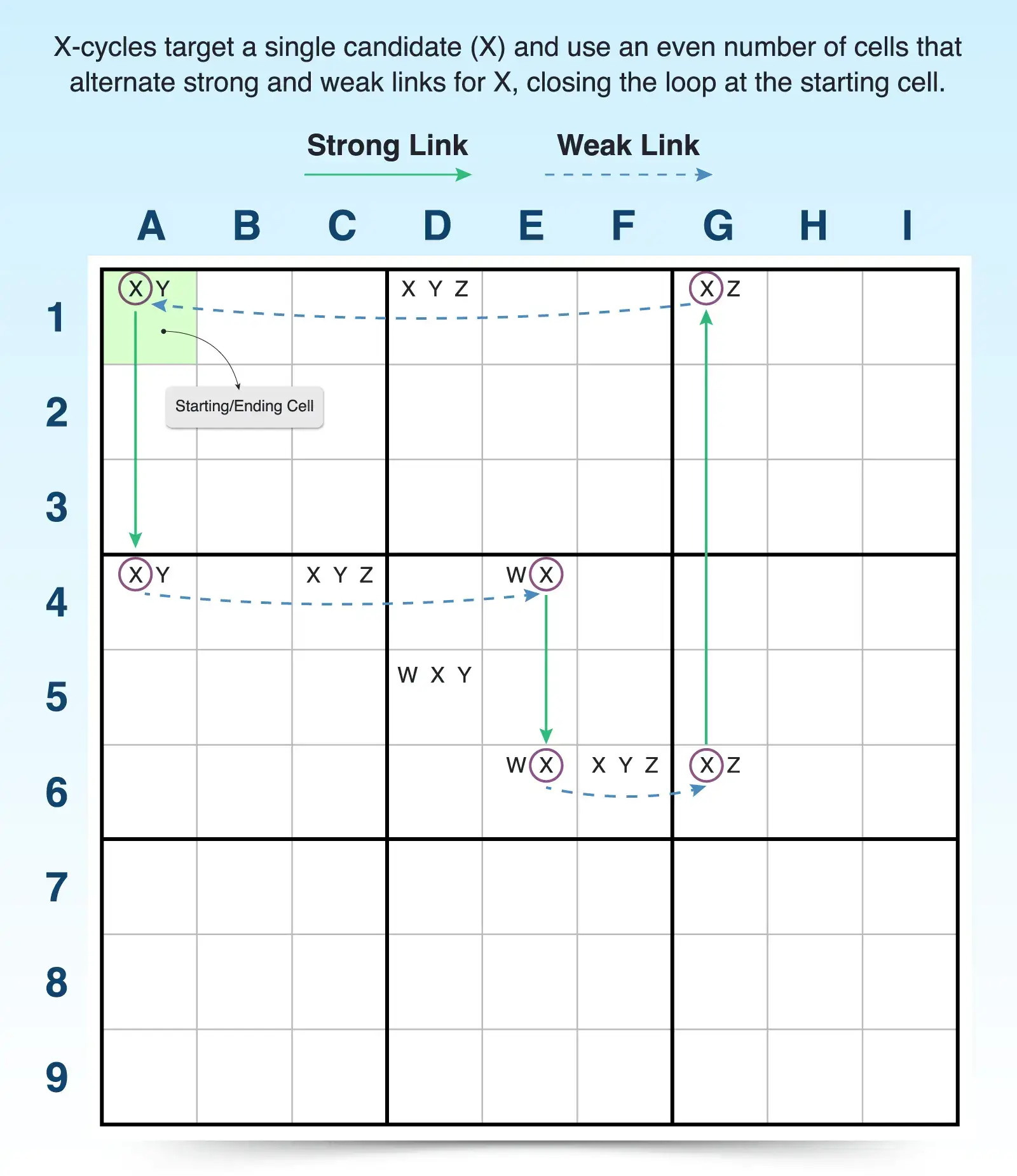
• Focus on a single digit: X-cycles are single-digit chains. All links in the chain represent candidate positions for the same digit (candidate x) and the logic of the chain applies only to that digit. For example, the grid below traces the links between candidate 7 in the puzzle.
• Alternate between strong links and weak links. The cycle must strictly alternate between strong and weak links. Strong links offer a strong inference: if one candidate is false, the other must be true. Weak links offer a weak inference: if one candidate is true, the other must be false. This alternating sequence ensures logical flow. For example, A1 to A4 is strong; A4 to E4 is weak; E4 to E6 is strong; E6 to G6 is weak; G6 to G1 is strong; and G1 back to A1 is weak. To alternate properly, you’ll find that X-cycles contain an even number of cells in the loop.
• Can flow in either direction. The type of link (strong or weak) remains the same regardless of the direction in which you trace the cycle. This means you can analyze the loop from any point and still apply the logic of the link consistently. For example, A1 to G1 is weak; G1 to G6 is strong; G6 to E6 is weak; E6 to E4 is strong; E4 to A4 is weak, and A4 back to A1 is strong.
• Form a closed loop. The ends of the chain are in the same cell (A1). A valid X-cycle ends in the starting cell, forming a continuous loop. This closure is necessary for applying the elimination or placement rules based on link types and loop structure.

You can even find X-cycles in the logic behind other solving techniques like X-wings and some swordfish patterns.

Examples of How to Use the X-Cycle Sudoku Technique

X-cycles follow strict linking rules that lead to helpful conclusions, even in expert level puzzles, allowing you to eliminate a candidate from one or more cells.

Remember that strong links make something true and weak links make something false. X-cycles combine both types of links to trap logic in a loop to make an outcome certain. These sections walk you through an example of each type using the X-cycle rules.

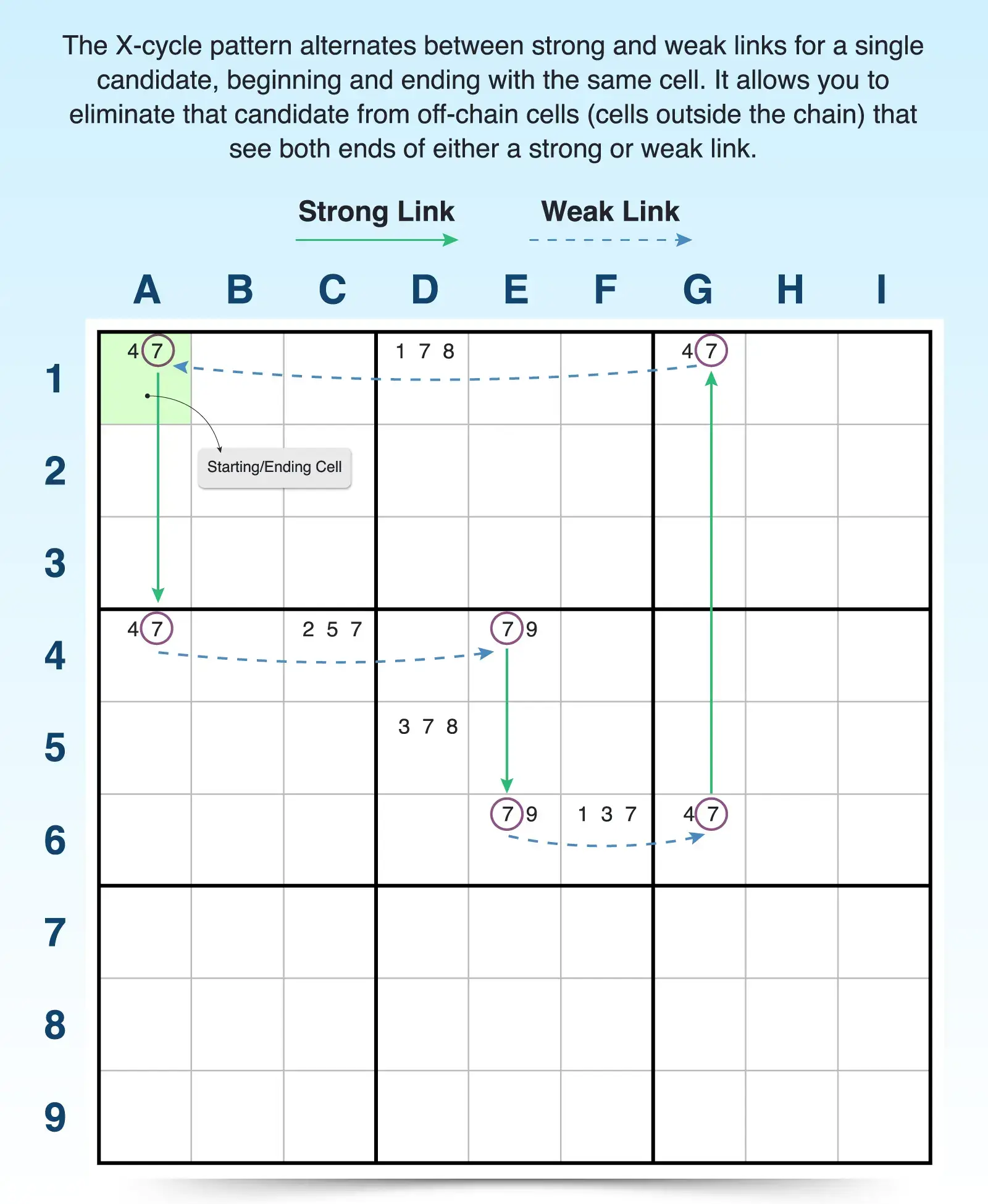
X-Cycle Rule 1: Elimination with a Weak Link

With the first X-cycle rule, you can eliminate a candidate based on a weak link that is flanked by two strong links in the cycle. If the X-cycle contains a weak link between two cells, then one of the weak-link endpoints must be true if it’s flanked by two strong links. So any cell that sees those two weak-link endpoints cannot contain the candidate targeted in the X-cycle.

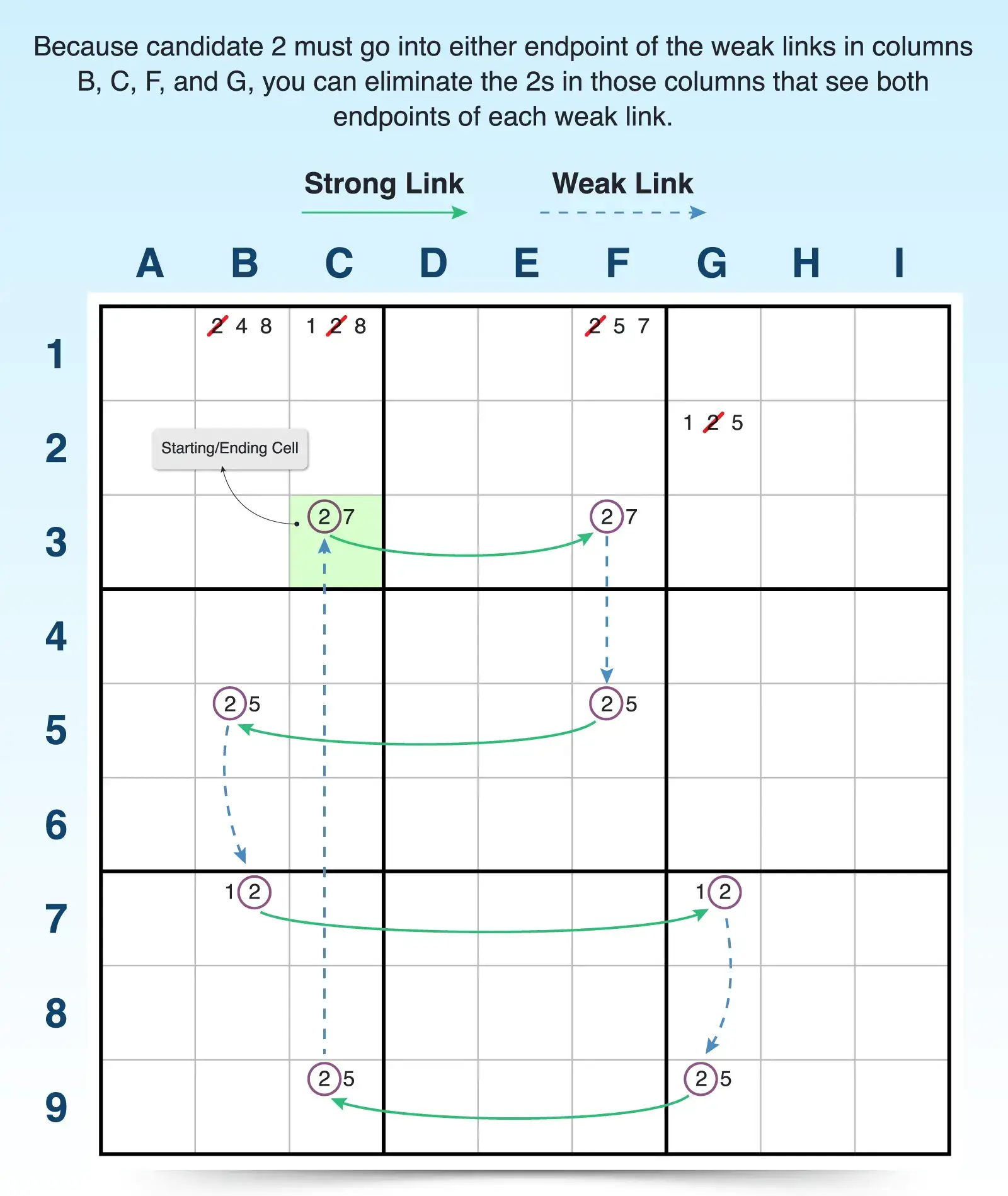
For example, F3 and F5 are both endpoints of a weak link flanked by strong links on each end (C3 to F3 and F5 to B5). So 2 must be the answer to either F3 or F5. Thus, any cell that sees both F3 and F5 cannot have a candidate 2. This allows you to eliminate candidate 2 from F1. Following the same logic, you can eliminate candidate 2 from B1, C1, and G2 as well.

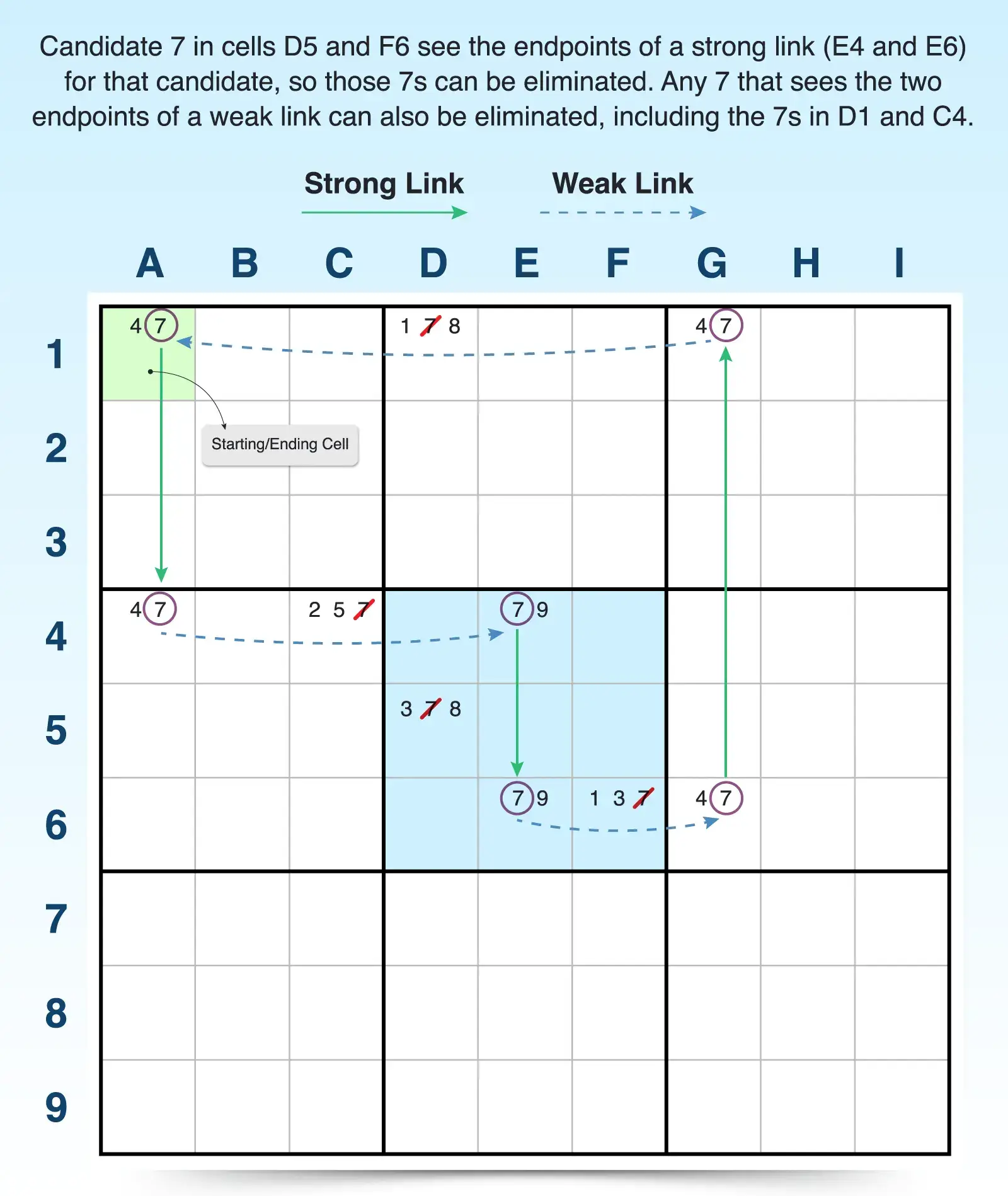
X-Cycle Rule 2: Eliminations with a Strong Link

With the next X-cycle rule, you can eliminate candidates that see both ends of a strong link. With a strong link (conjugate pair), the candidate must be the answer in one of those cells. If the same candidate in another cell sees both of those endpoints, you can eliminate the candidate from that other cell.

For example, cells D5 and F6 contain the target candidate 7, and they share a 3x3 block with the endpoints from the strong link for candidate 7 (cells E4 and E6). Because 7 must be the answer to either E4 or E6, you can eliminate candidate 7 in any cells that see both E4 and E6. Knowing what you know about X-cycle Rule 1, you can also eliminate any 7 that sees two endpoints of a weak link.

Using logical Sudoku strategies like X-cycles can help you eliminate candidates and have you solving puzzles faster when you play Sudoku online.