Sudoku Tips and Strategies

Sudoku is a logic puzzle full of numbers but no math, offering challenges for every skill level-you can even find Sudoku puzzles for kids! But no matter whether you're a beginner working your way through an easy puzzle or have the experience to tackle grids on an evil level, you can solve puzzles more efficiently and easily by following Sudoku strategies.

Sudoku strategy gives you a logical way to work through puzzles, especially when you get stuck. With this post, you can find the perfect Sudoku strategy to match your skills and experience and learn how to use new Sudoku techniques to level up your skills.

Sudoku Strategy for Beginners

Most of the Sudoku strategies for easy puzzles focus on scanning the puzzle for possibilities. Once you've exhausted those strategies, you can try techniques that explore puzzle analysis, suitable for some easy as well as medium puzzles.

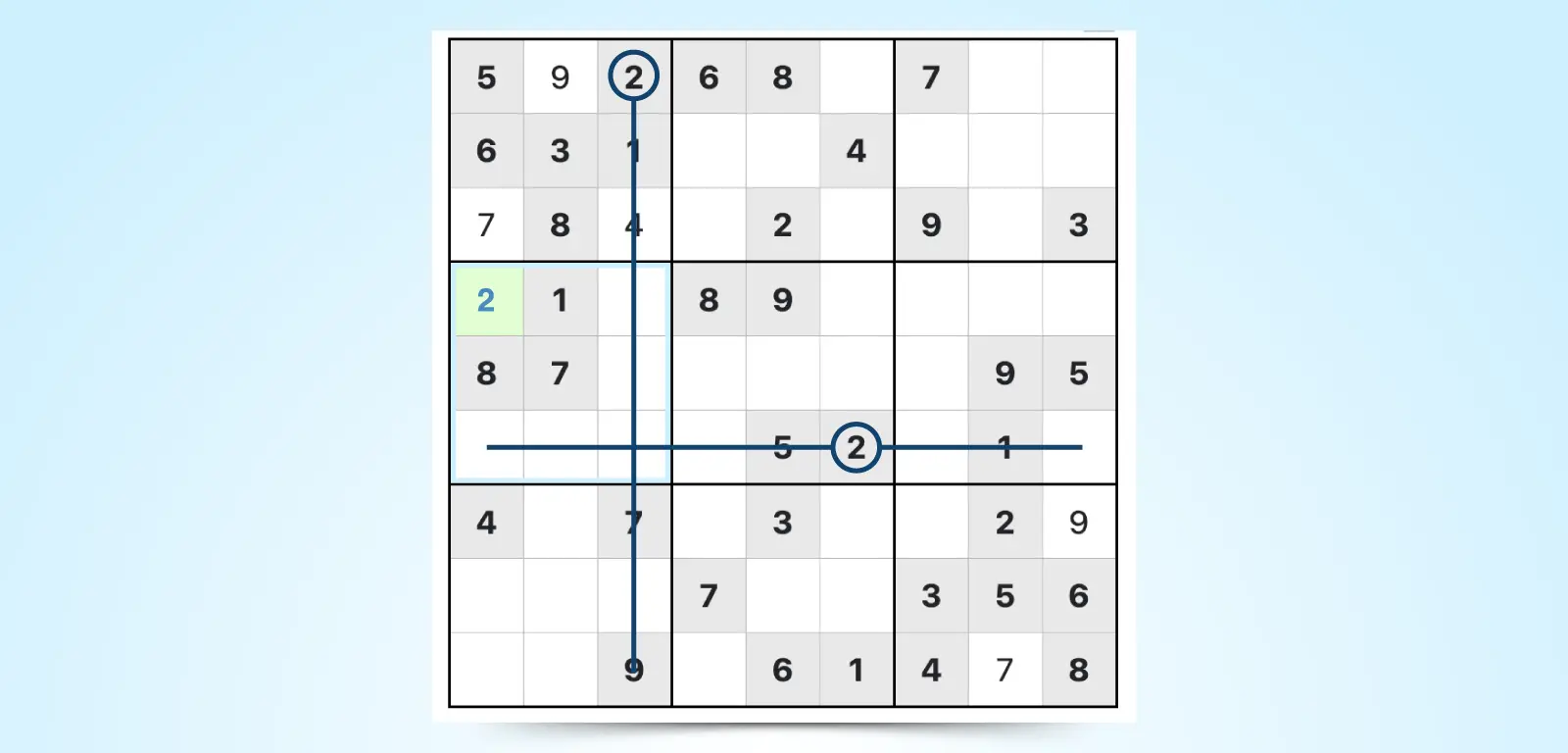
1. Cross-Hatching

Cross-hatching is a basic Sudoku solving technique used to scan for possible number placements. You look at a specific candidate number (2) and draw a line through each row and column to eliminate where that candidate can't go.

Because you can't have a 2 in the same row or column where a 2 is already placed, cross-hatching helps you narrow down the options, often to a single valid cell. This early-game strategy allows you to find more obvious openings for numbers.

cross-hatching sudoku strategy example

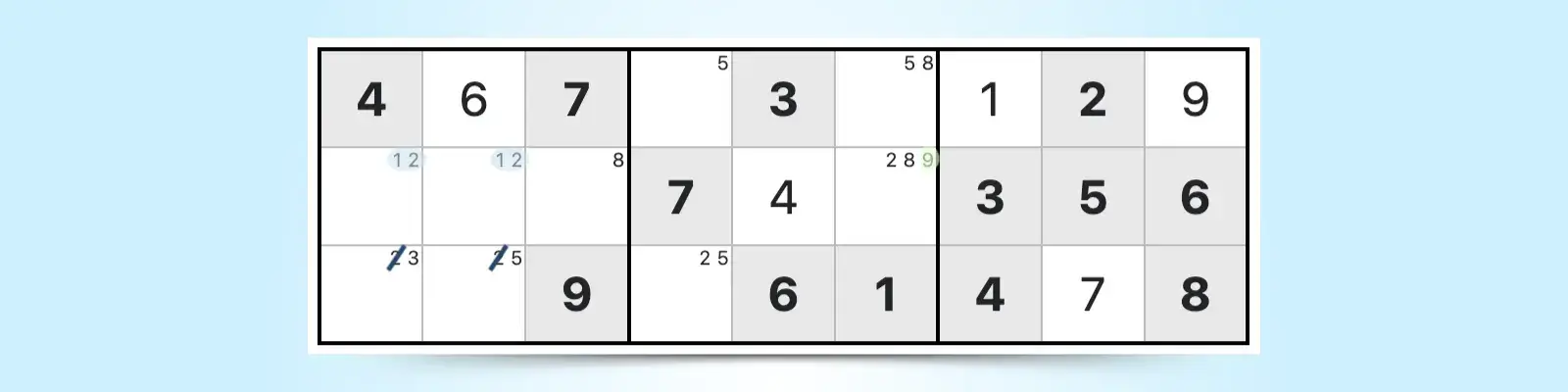
2. Pencil Marks (Candidate Numbers)

Pencil marks refer to literally using a pencil to mark candidate numbers on a paper puzzle. Digital games offer this feature too. On Sudoku Bliss, you can check the "This number is a possibility" box to mark possible candidates.

Noting the candidate numbers with pencil marks throughout the entire puzzle is an important technique to perfect early on. Pencil marks allow you to utilize other techniques so that you can eliminate candidates or discover answers to cells throughout the puzzle.

pencil marks sudoku strategy example

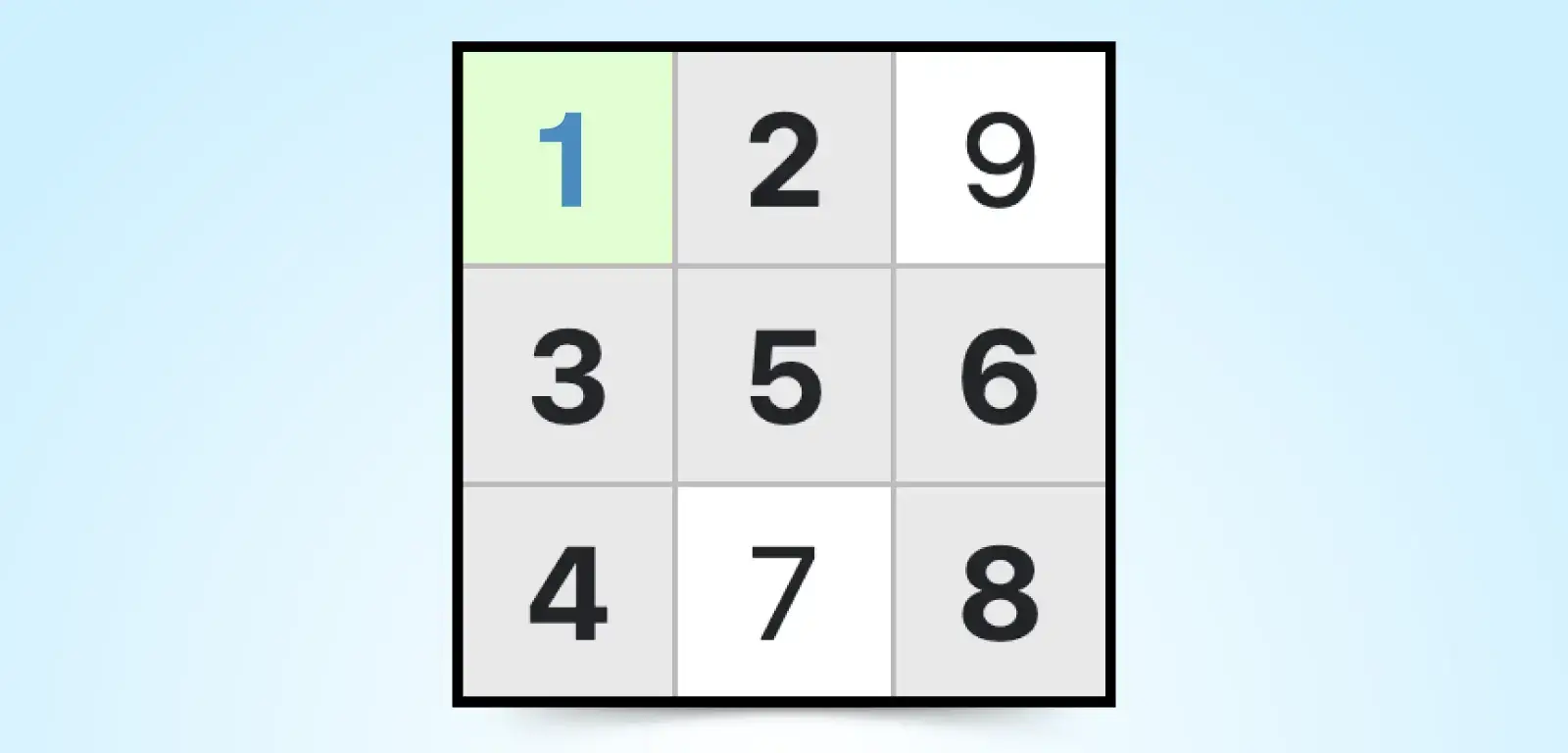
3. Naked Single

A naked single in Sudoku means an empty cell has only one possible candidate number. You may notice this right after using pencil marks or after you've used other elimination techniques that rule out other digits for that cell.

For example, because 1 is the only number that can go in the top left cell, that must be the answer for that cell. Naked singles are usually the easiest and most straightforward placements to find.

naked single sudoku strategy example

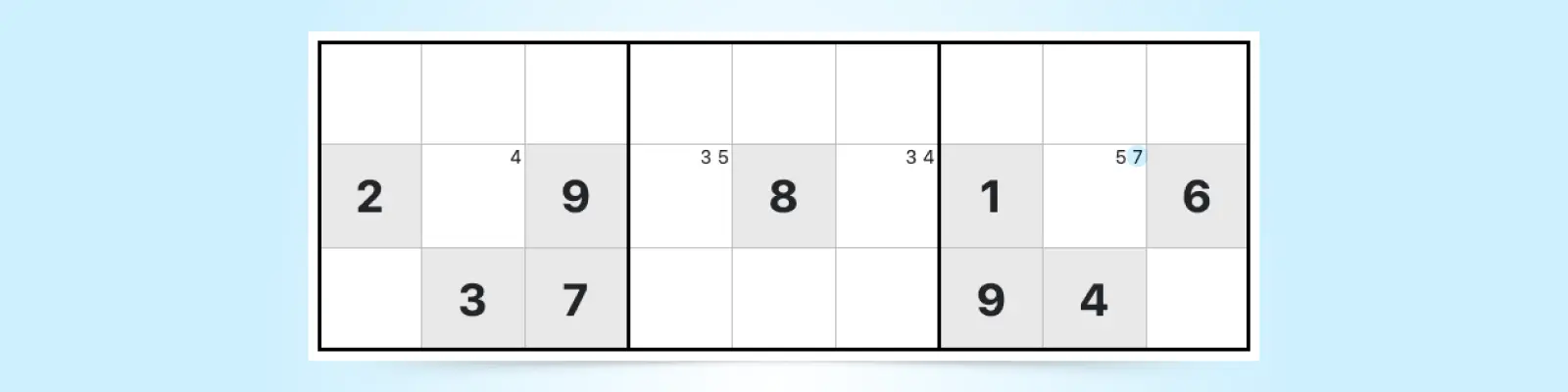
4. Hidden Single

Hidden singles are just a slight step up from finding naked singles. A hidden single is still the only possible candidate for a cell, but it's more difficult to find than a naked single because other candidates are hiding the single in a cell.

You can find a hidden single by focusing on a number and then scanning rows and columns to see if the number is marked just once as a candidate. For example, the 7 is a hidden single because it's the only 7 in that row, so the 7 must be the answer to that cell. It's hidden because the 5 candidate also appears in that cell.

hidden single sudoku strategy example

Sudoku Strategy for Intermediate Solvers

If you're experienced with beginner strategies, you can start using intermediate techniques that stay focused on puzzle analysis. These strategies can help you fill in missing numbers efficiently to solve medium Sudoku puzzles.

5. Naked Pair

A naked pair in Sudoku is when two cells in the same row, column, or block contain exactly the same two candidates, and only those two candidates. This means those two numbers must go in those two cells-even if you don't yet know which goes where.

As a result, those two candidates can be eliminated from all other cells in that same unit (row, column, or block), because no other cell can logically have those numbers as an answer. This technique allows you to narrow down possibilities and make progress, especially in hard Sudoku puzzles where singles aren't typically available.

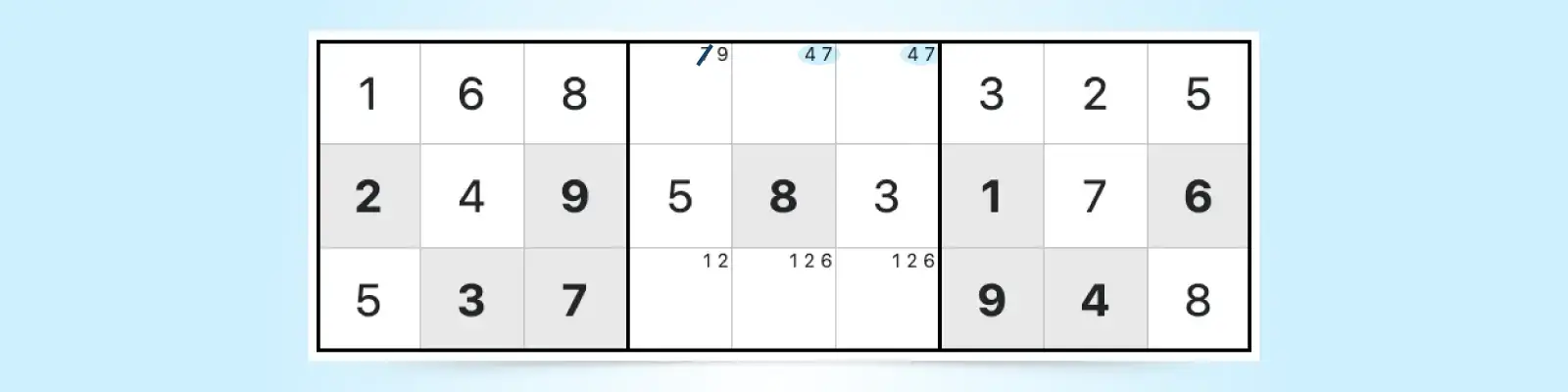
naked pair sudoku strategy example

6. Hidden Pair

A hidden pair occurs when a pair of candidates appear only in two cells within a row, column, or block, but unlike the naked pair, those cells contain other candidates as well. This allows you to eliminate all other candidates from those two cells, leaving just the hidden pair.

hidden pair sudoku strategy example

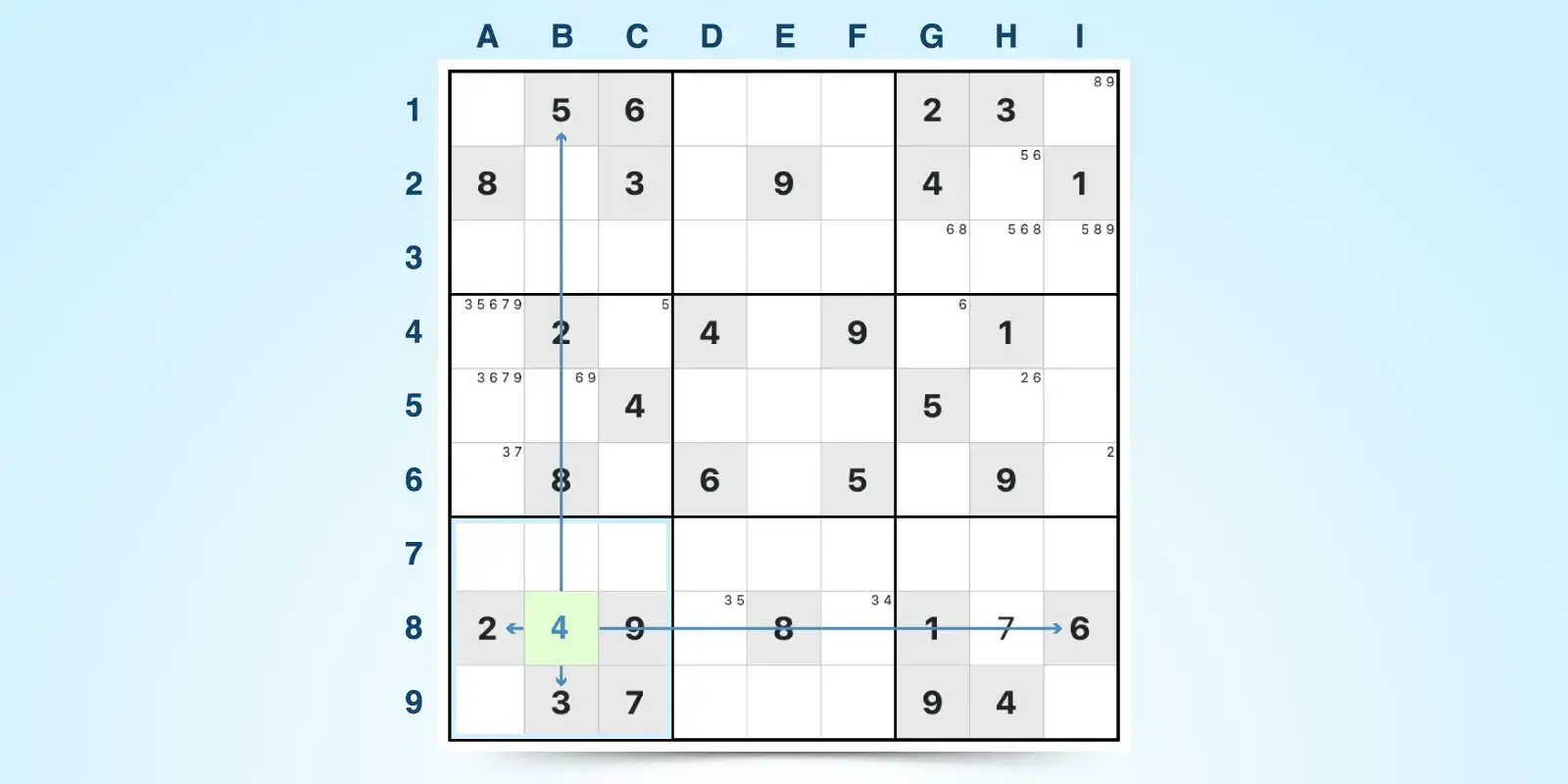
7. Last Possible Number

The last possible candidate technique in Sudoku refers to a situation where only one number can possibly go into a specific cell-not because it's a naked single, but because it's the only place left for that number based on the answers in the surrounding row, column, and block.

last possible number sudoku strategy example

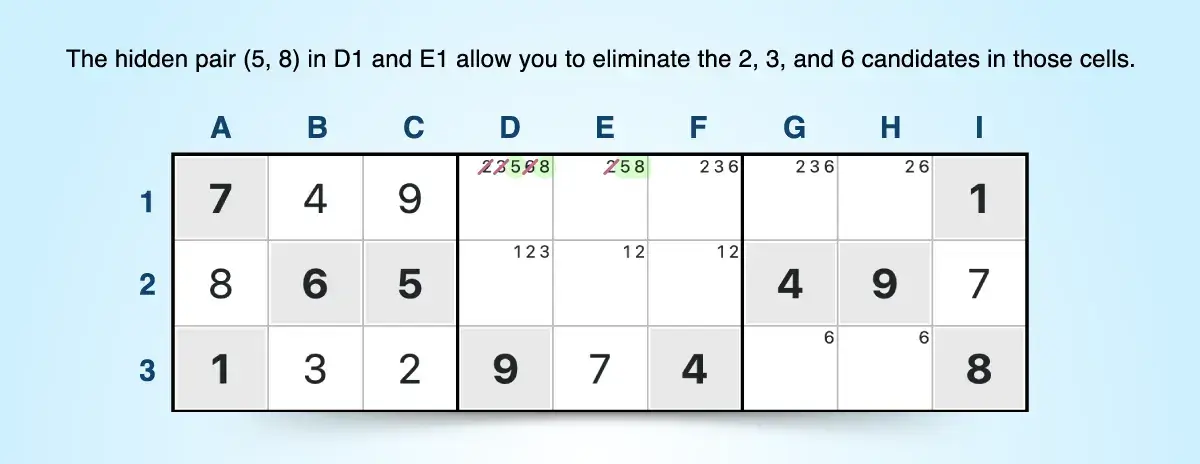
8. Naked Triple

A naked triple is where three cells in the same row, column, or block contain only three candidates total-and no other numbers. Each cell can have two or three of the candidates, but together they include only three specific numbers. Because these three numbers must go in those three cells in some order, they can be eliminated from the rest of the unit.

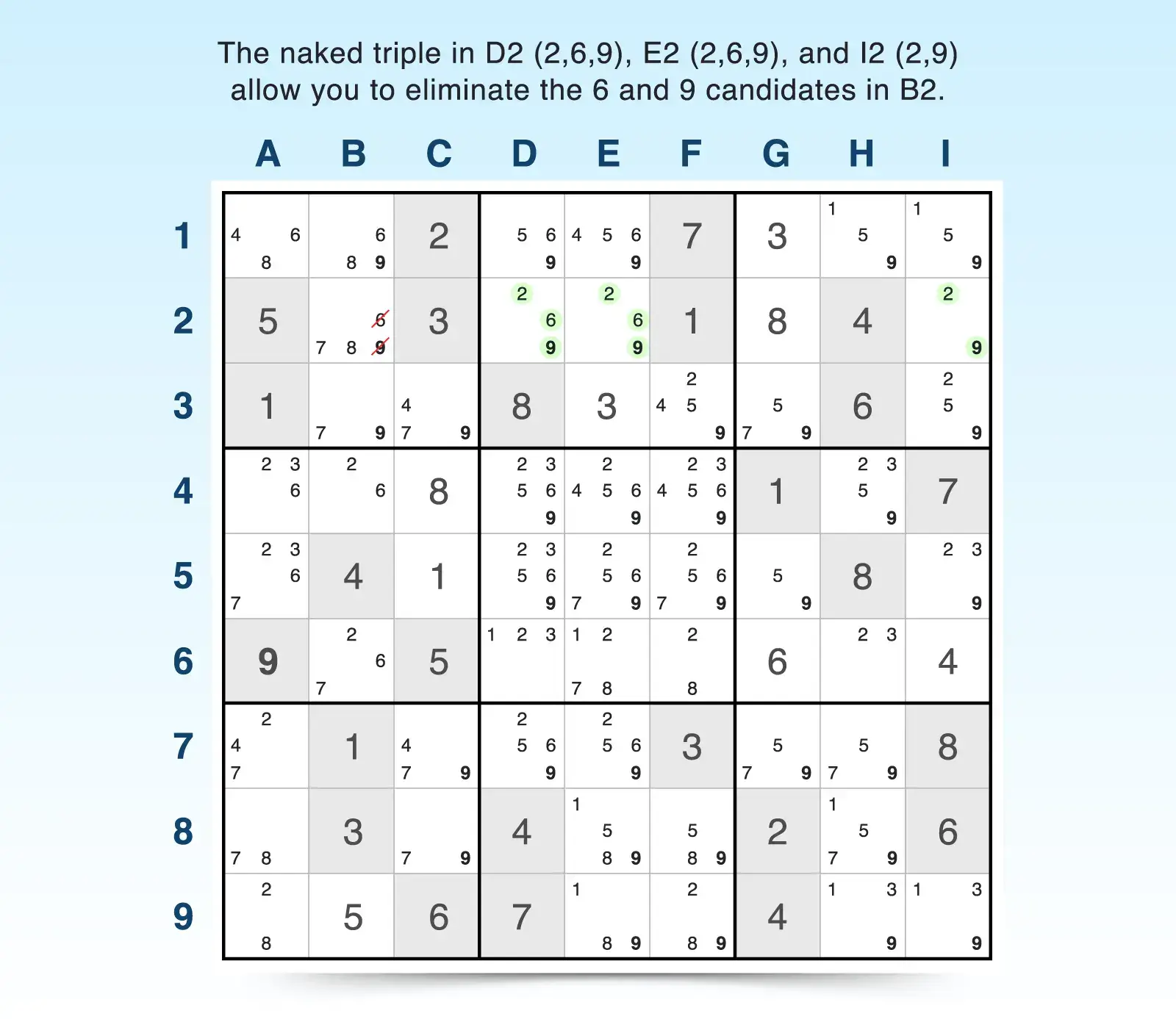
naked triple sudoku strategy example

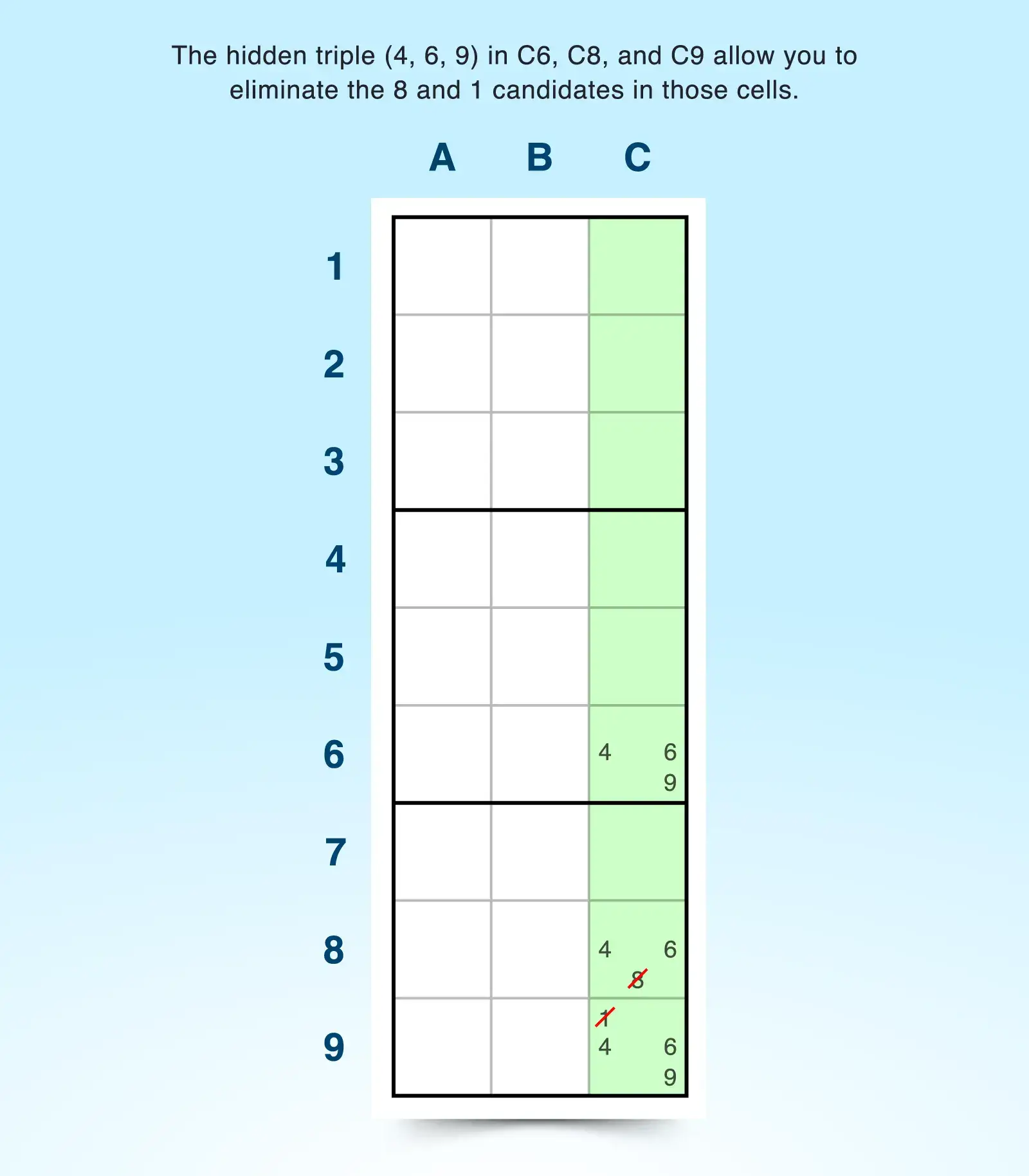
9. Hidden Triple

A hidden triple happens when three specific candidates appear only in three cells within a row, column, or block-but those cells may also contain other candidates. Typically, not all three candidates will be present in each of the three cells. Some cells may have only one or two of the numbers. The key is that only three cells in a unit can contain a combination of the three specific numbers, so any other candidates in the same cells can be removed.

hidden triple sudoku strategy example

Sudoku Strategy for Advanced Solvers

When you're ready to step up your solving skills, you're not just ready for hard puzzles, but you're also ready for more advanced strategies. These strategies offer a deeper analysis of your puzzles, revealing candidates that can be eliminated to narrow down answers for cells.

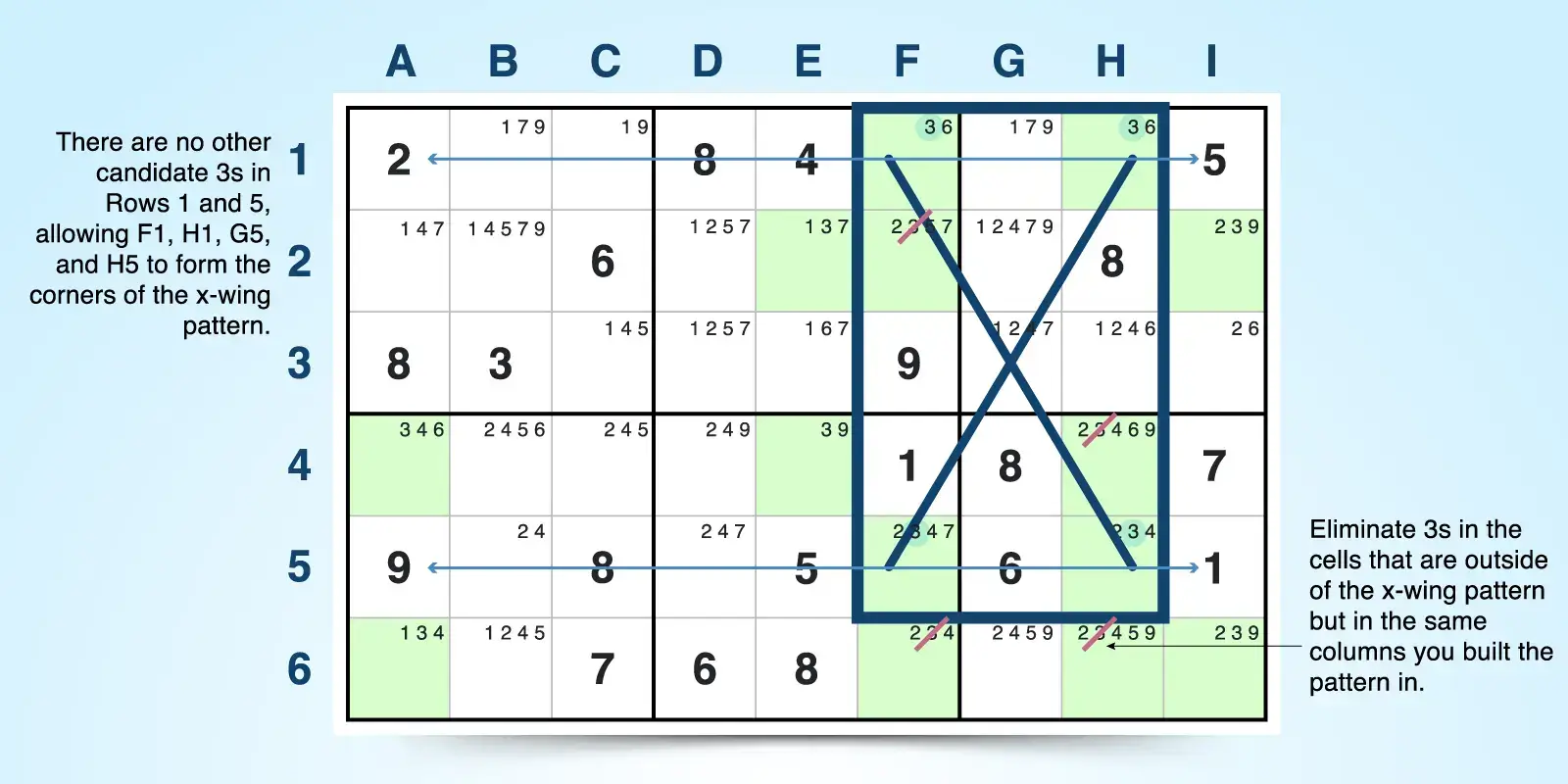
10. X-Wing

The X-wing strategy helps you eliminate candidates by spotting a pattern of four cells containing the same candidate that forms a rectangle. To use this technique, look for two rows (or two columns) where a certain number appears in exactly two cells in each row (or column)-and those cells line up in the same columns (or rows). These four cells form the corners of a rectangle, and you can draw diagonal lines from corner to corner to form an X.

Because the candidate must occupy one of the two aligned cells in each row (or column), it cannot appear in any other cells within those same columns (or rows). This lets you eliminate that candidate from all other cells outside the X-wing pattern in those columns (or rows).

X-wing sudoku strategy example

11. Swordfish

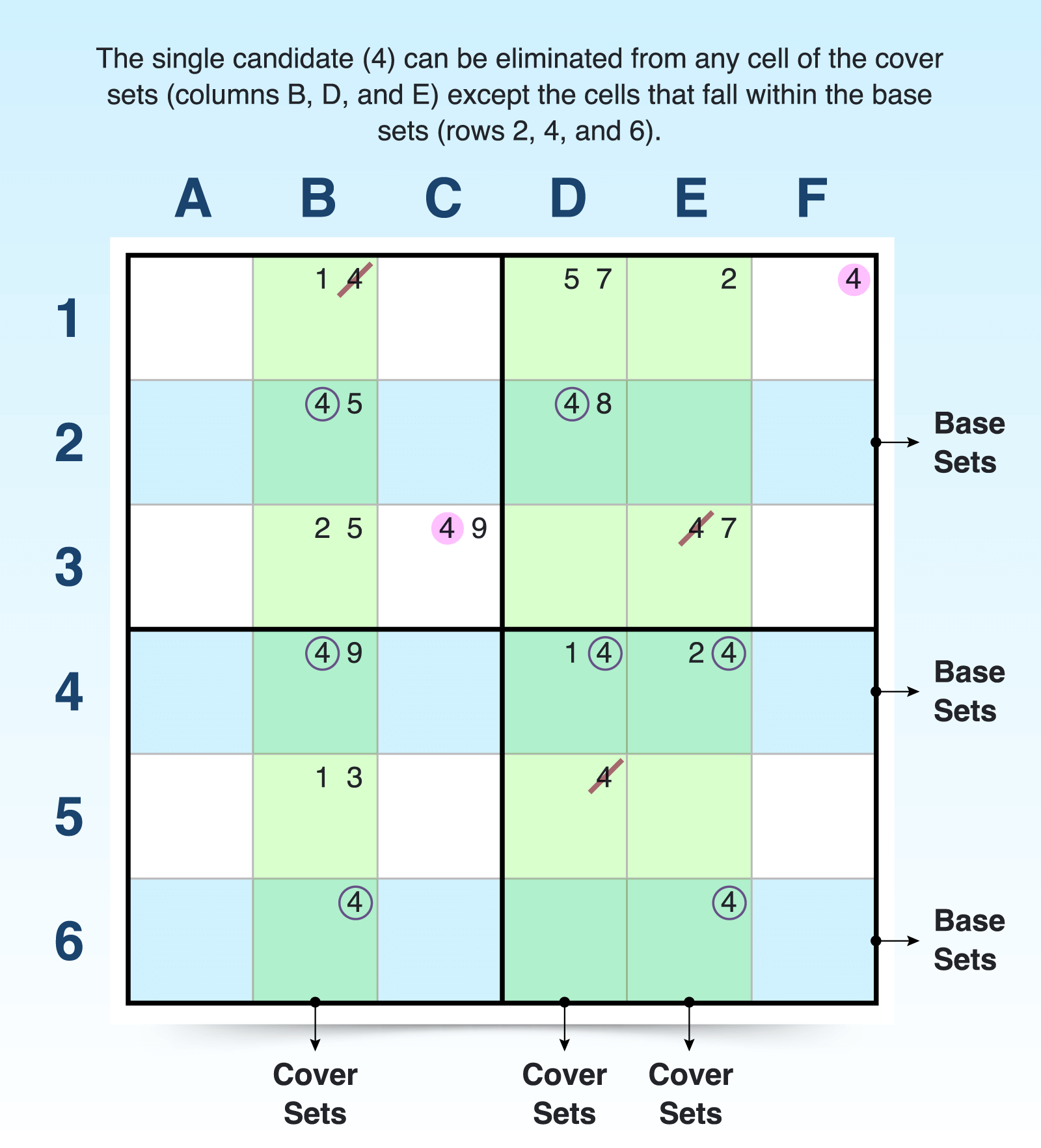
The swordfish strategy is like an extension of the X-wing. Instead of using two rows and two columns, it works with three rows and three columns.

Start by picking one candidate number. In each of the three rows (or columns), that number should only appear in two or three cells and nowhere else in those rows (or columns) to create your base sets. Those cells should then line up in the same three columns (or rows) to form your cover sets.

Because the candidate number must go somewhere in the selected cells, you can remove it as a candidate from any other cells in the cover sets outside the swordfish pattern.

swordfish sudoku strategy example

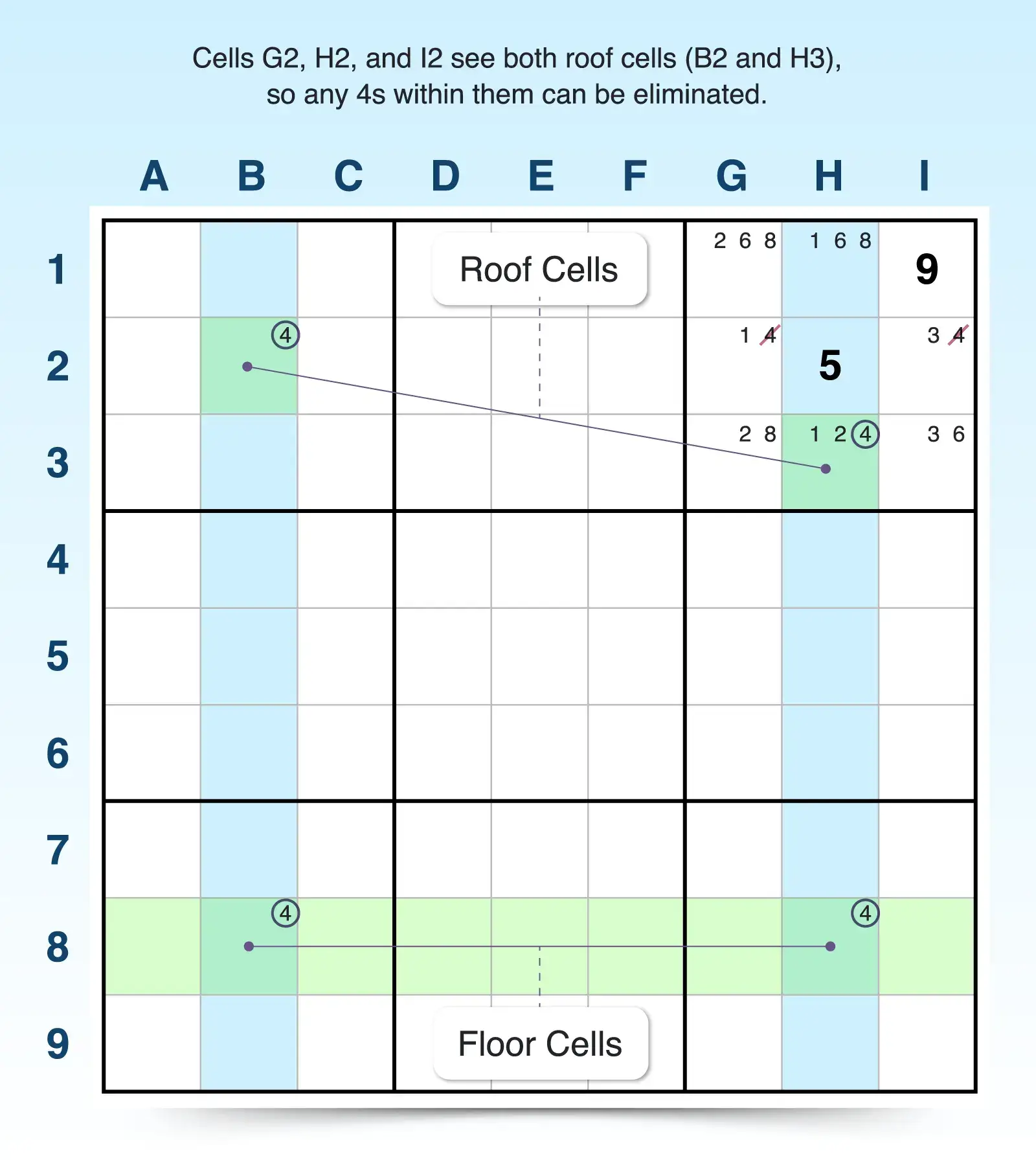
12. Skyscraper

The skyscraper strategy is similar to the X-wing. Focus on a candidate and see if it appears in exactly two cells in two different rows (or columns), for a total of four cells. Two of the four cells must align in one column (or row) to form the floor of the skyscraper while the other two must appear in two different columns to form a slanted roof-hence the name.

Because one of the roof cells must be true, you can eliminate that candidate from any cell that sees both roof cells. The skyscraper can be formed in all directions. So the floor could be formed in rows with the roof pointing left or right, or the floor could be formed in columns with the roof pointing up or down.

skyscraper sudoku strategy example

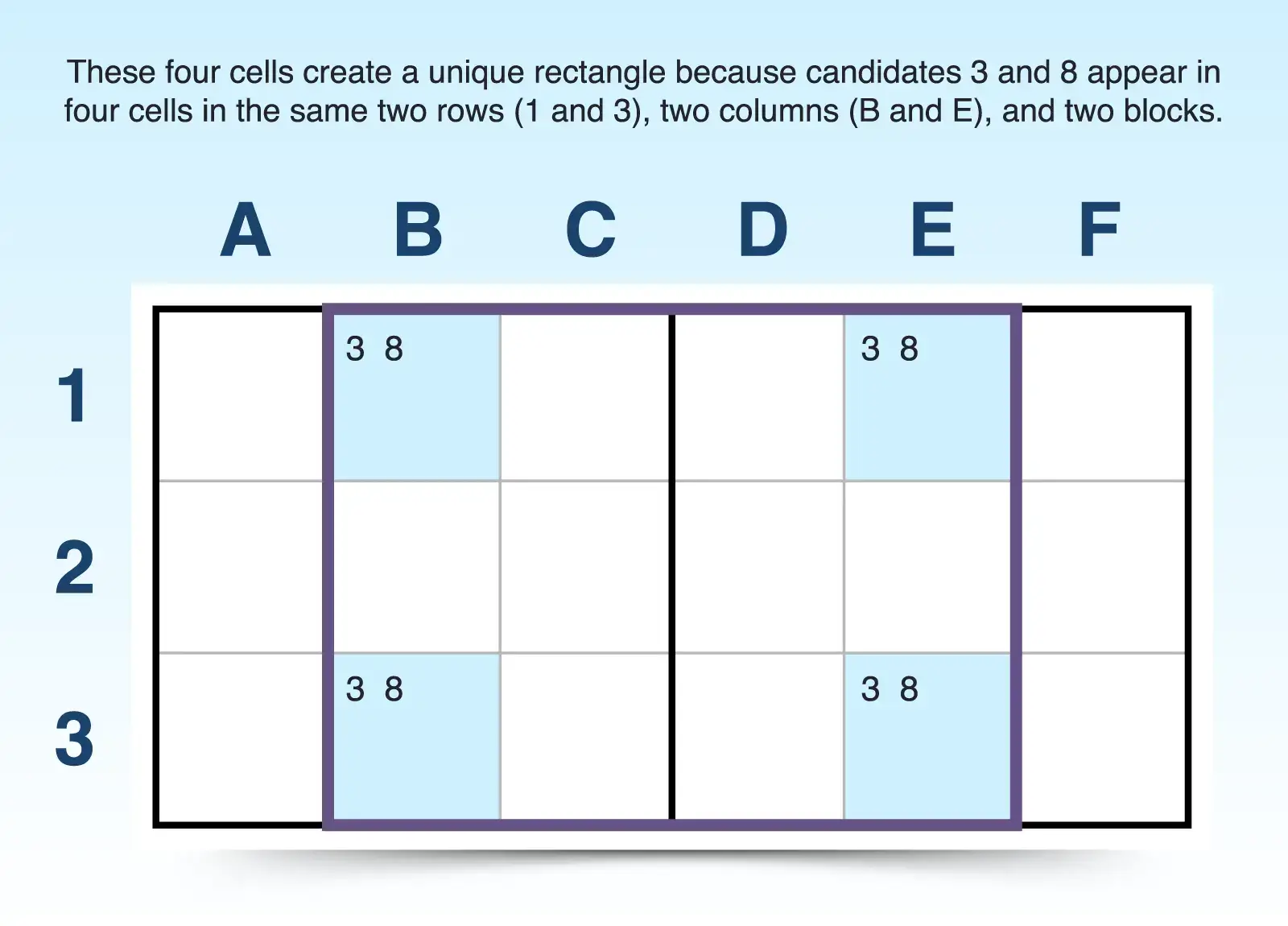
13. Unique Rectangle

The unique rectangle strategy relies on the rule that every Sudoku puzzle has only one solution. If four cells form a rectangle and all share the same two candidates-spanning exactly two rows, two columns, and two blocks-they could create two different solutions, which breaks the logic of the puzzle.

To spot one:

  1. Look for two cells in the same row (or column) that share the same two candidates. It doesn't matter if the cells have other candidates, and the two candidates can appear elsewhere in the row (or column).
  2. Then look at a different row (or column) and find two more cells with the same pair of candidates that line up in the same columns (or rows) as the other two cells.
  3. Make sure these four cells fall into just two 3x3 blocks.

If all four cells contain only those two candidates, that creates a "deadly rectangle"-an illegal situation. Since this can't happen in a valid puzzle, you need a way to break the pattern and eliminate options. Sudoku has five types of unique rectangles all with different ways to break the deadly pattern.

unique sudoku strategy example

14. Locked Candidates

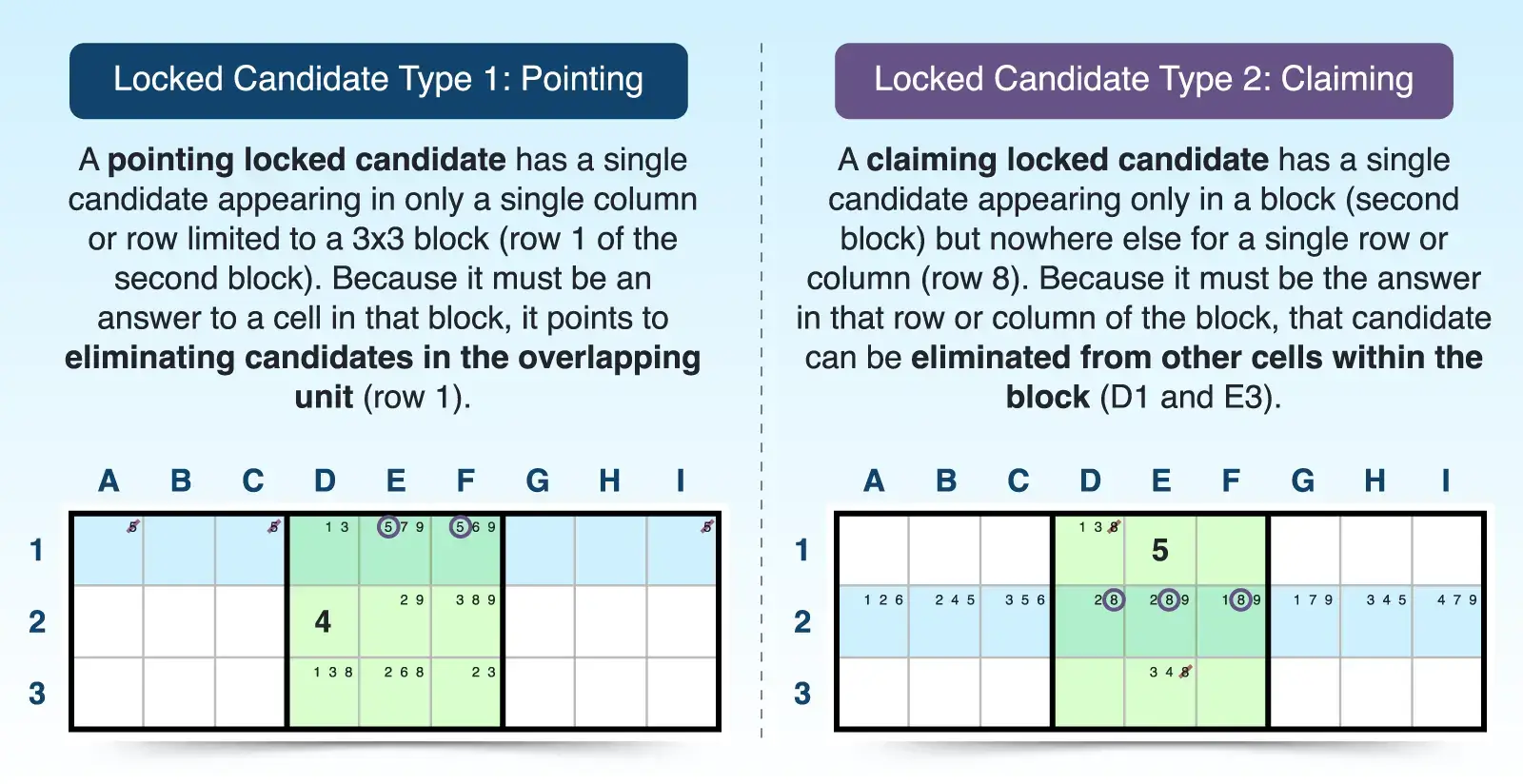
The locked candidates strategy allows you to eliminate numbers based on where a candidate is restricted within overlapping units-rows, columns, and blocks. This restriction is why it's called a "locked" candidate-the number is locked into part of a row or column inside a block, which helps you rule it out elsewhere. How the candidate is situated within these units determines what type of locked candidate you have and how you can make eliminations.

If you find a single candidate that only appears in one row or column within a 3x3 block and nowhere else in that block, that candidate must be the answer in that row or column inside the block. This is a type 1 locked candidate, called a pointing locked candidate. Because that candidate can't be the answer in that same row or column outside the block, you can eliminate that candidate from the rest of the row or column beyond the block.

If a candidate appears in a 3x3 block but nowhere else in a particular row or column, it must be the answer in that row or column within that block. Because the candidate doesn't appear elsewhere in the single row or column, it is a type 2 locked candidate, called a claiming locked candidate. You can eliminate it from elsewhere in the block aside from the row or column in which it must be the answer.

locked candidates strategy example

Sudoku Strategy for Experts

Some Sudoku solvers need an extra challenge, and expert Sudoku strategies can help you confirm or eliminate candidates effectively to solve puzzles at the expert and evil level.

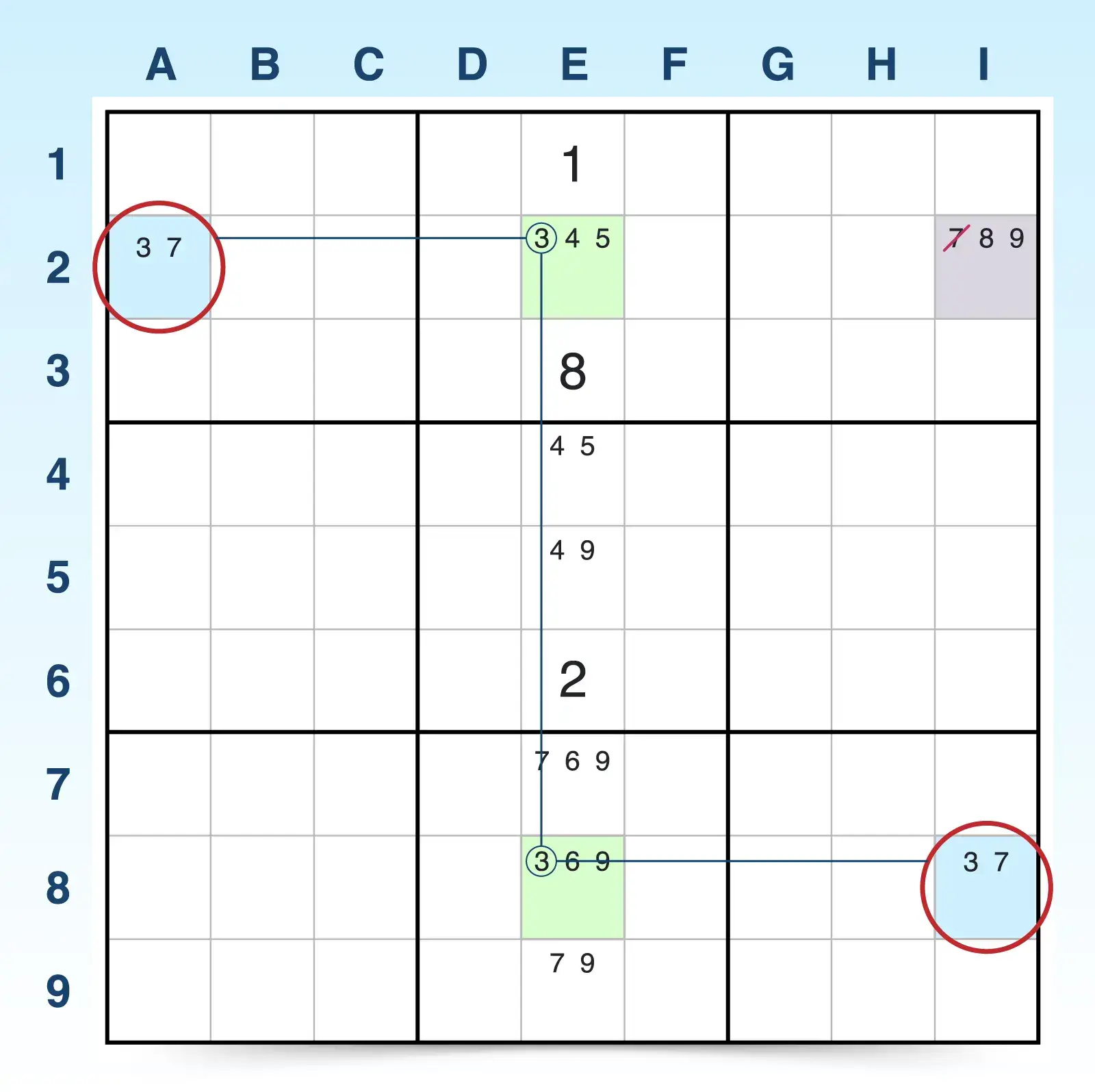
15. W-Wing

The W-wing strategy helps you eliminate a candidate based on a chain of four cells that starts and ends with two matching bi-value cells. The two cells between them must contain a strong link between one of the bi-value cells' candidates. Sometimes a W-wing doesn't lead to an elimination, but you can find one quickly and easily, so it's a good strategy to use first when you're stuck with a more difficult puzzle.

To find a W-wing, make sure the following is true:

  1. Find two bi-value cells (cells with exactly two candidates) that contain the same pair of numbers. Think of the candidates as x and y. These two bi-value cells must not see each other-they can't be in the same row, column, or block.
  2. Look for a strong link (a conjugate pair) for one of the candidates (x), where each of the two linked cells sees a different bi-value cell. A strong link means that the candidate (x) appears in exactly two places in a row, column, or block. This strong link should connect two cells, and each one should see one of the bi-value cells.
  3. Eliminate the other candidate (y), if possible. If the other candidate (y) appears in any cell that sees both bi-value cells, you can eliminate it from those cells.
W-wing candidates strategy example

16. XY-Wing (Y-Wing)

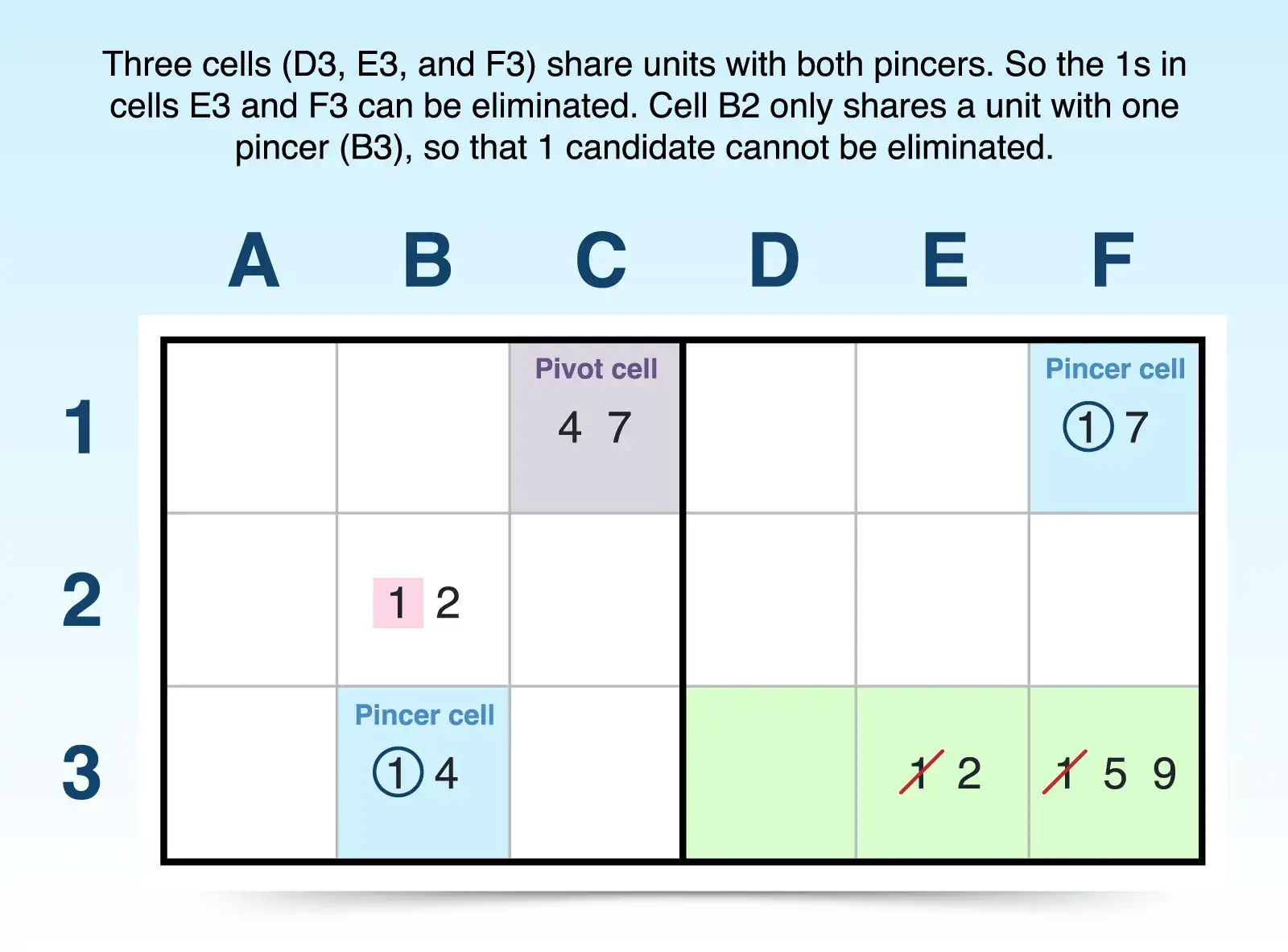
The Y-wing (or XY-wing) is a technique that uses three bi-value cells-one pivot cell and two pincer cells-to eliminate candidates. Although the strategy is called a Y-wing, it doesn't refer to the shape of the pattern. In fact, the reason some Sudoku solvers refer to it as XY-wing is because you think of the candidates in the pivot cell as (x, y).

To find the Y-wing pattern, see if you have the right combination of bi-value cells:

  • One pivot cell: This bi-value cell should contain candidates x and y.
  • First pincer cell: This bi-value cell should contain candidates x and z. This cell not only shares one candidate with the pivot cell, but it should also share one unit (row, column, or 3x3 block).
  • Second pincer cell: This bi-value cell should contain candidates y and z. This cell also shares a unit with the pivot cell, but it cannot share a unit with the first pincer cell.

If you find these three cells under these conditions, then you can eliminate candidate z from any cells that both of the pincer cells can see (cells that share a unit with both pincer cells).

XY-wing candidates strategy example

17. XYZ-Wing

The XYZ-wing technique builds on the XY-wing strategy by adding another candidate to the pivot cell. So instead of three bi-value cells, you have one cell with three candidates (x, y, and z) that acts at the pivot cell, and then two bi-value pincer cells.

So the XYZ-wing pattern follows these criteria:

  • Pivot cell: This cell contains three candidates (x, y, and z).
  • First pincer cell: This cell contains two candidates (x, z) and shares a unit with the pivot cell.
  • Second pincer cell: This cell contains two candidates (y, z) and shares a unit with the pivot cell, but it doesn't share a unit with the other pincer cell.

Because all three cells in the pattern now share candidate z, you can eliminate that candidate from any cell that all three cells can see (any cell that shares a unit with all three cells).

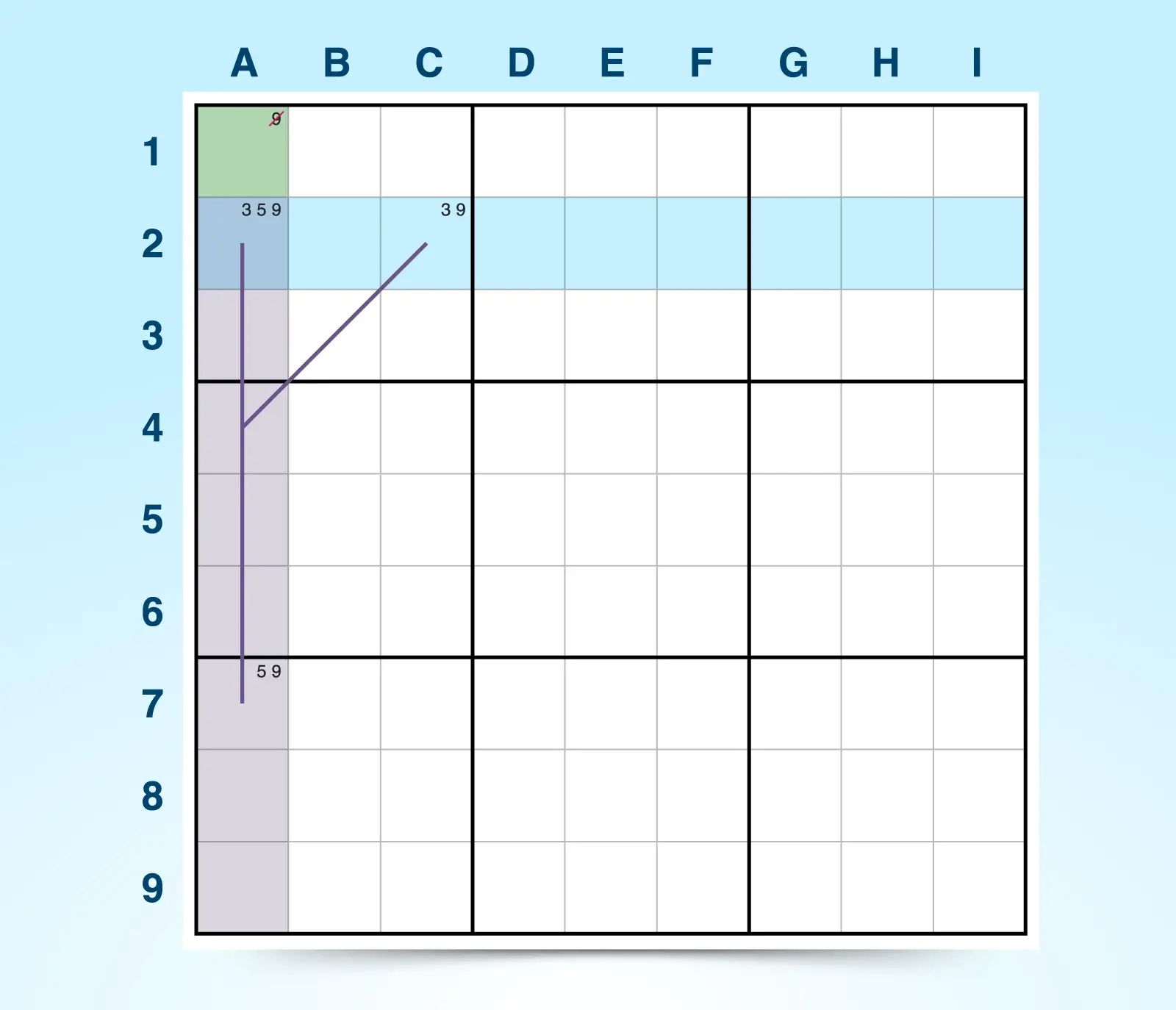
XYZ-wing candidates strategy example

18. Forcing Chains

The forcing chains strategy is a subset of alternating inference chains (AIC). To use this technique, you simply follow the logic of what would happen if each candidate in a starting cell is the answer for that cell. By following the chain reaction of answers for each candidate, you can confirm an answer in the last cell of the chain, confirm candidates and eliminate others from the last cell, or discover a contradiction of logic that eliminates a candidate from the starting cell.

This strategy uses if-then logic, not guesswork to narrow down answers in the puzzle. The simplest way to practice this technique is to use a chain reaction of bi-value cells. If you assume that one is the answer, you follow the path of answers it creates and note how the chain ends. Then you assume the other candidate is the answer in the starting cell to see how that chain of answers ends. What you conclude gives you clues on how to eliminate candidates:

  • If both assumptions end with the same conclusion, you can confirm that the conclusion in the last cell must be true.
  • If both assumptions end with a different conclusion, you can conclude that both candidates in the last cell are possible candidates, allowing you to eliminate other candidates from the cell.
  • If an assumption results in a contradiction, you can conclude that the assumption is wrong and eliminate that candidate from the starting cell.
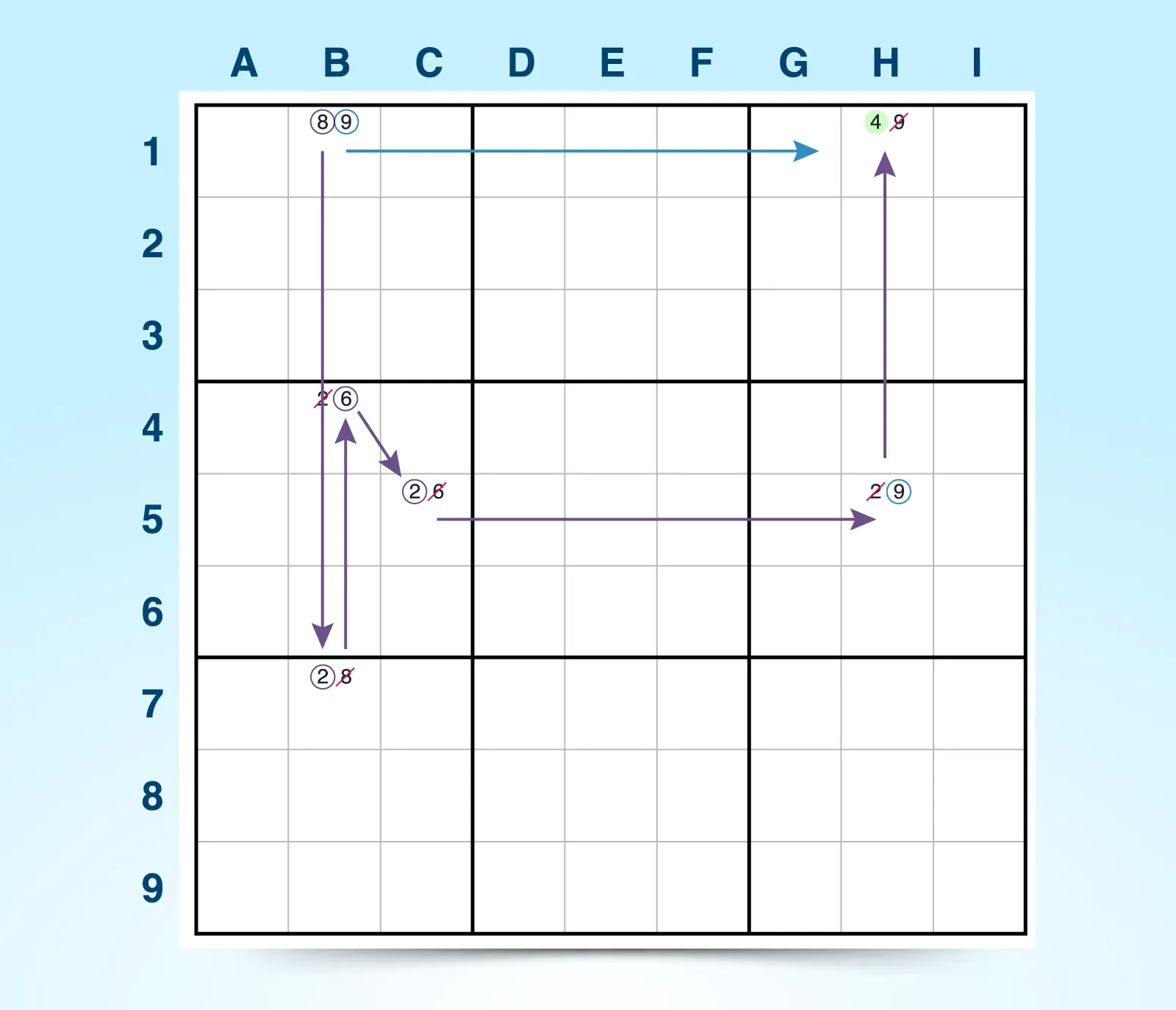
forcing chains strategy example

19. ALS-XZ

The ALS-XZ strategy uses the relationship between two sets of almost locked sets (ALS) sharing a common candidate to eliminate one or more candidates. An almost locked set has just one more cell than possible candidates in the group-N candidates in N+1 cells.

The XZ in the strategy, like many Sudoku strategies at this level, refer to candidate numbers. Using those letters as a guide, the following must be true for the two sets to be useful for elimination tactics:

  • ALS 1 and ALS 2 both share a restricted common candidate (X). This candidate appears only once in each set and must be the answer in one of the sets. In other words, the restricted common candidates in each ALS must see each other (share a unit).
  • ALS 1 and ALS 2 both share a common unrestricted candidate (Z). This candidate is found in both sets but is not restricted to be an answer in those sets.

If the above is true, then Z can be eliminated from any cell outside of those two almost locked sets as long as the cell sees candidate Z in all instances where it appears in both sets.

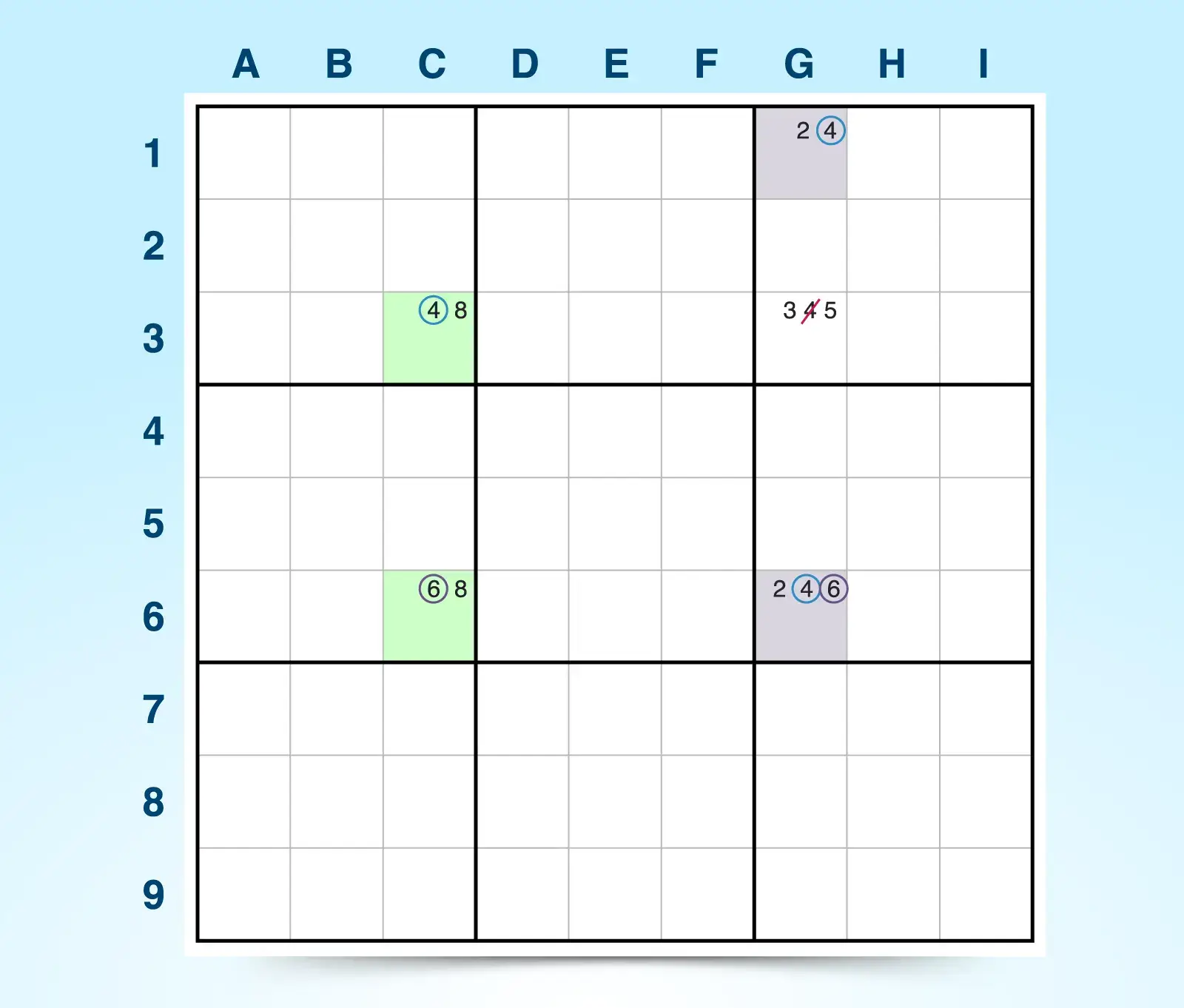
For example, column C has a locked set (ALS 1) with the restricted common candidate 6, and column G has another locked set (ALS 2) with the same restricted common candidate 6. The restricted common candidate in both instances connect both almost locked sets because they are in the same row. This connection helps to set up the elimination.

Because they both share one instance of the restricted candidate (6), and they both share a common candidate of 4 that is unrestricted, the 4 in G3 can be eliminated because it sees all 4s in the other cells in both sets that contain 4s.

ALS-XZ sudoku strategy example

Trying to solve puzzles through trial and error always ends in frustration, but solving techniques can offer you a logical path to working Sudoku puzzles. As you become comfortable with a new strategy, continue adding more methods to your Sudoku solving skills so that you can efficiently solve puzzles whenever you play Sudoku online.