Master the W-Wing Sudoku Technique: Examples and Tips

A W-wing is a Sudoku elimination technique that is easier to spot than other patterns like the X-wing or Y-wing. It's a chain that consists of four cells and meets the following criteria:

• The first and last cells in the chain must be identical bi-value cells containing candidates x and y. These cells cannot share a row, column, or block.
• The middle two cells must be a conjugate pair with a strong link between either x or y. A conjugate pair means that they are the only two cells within the same unit that contain the x or y candidate number.
• Each of the middle cells must share a unit with one of the bi-value cells.

This creates a logic chain that may help you eliminate candidates in cells that both the bi-value cells can see. Using the W-wing can help you solve all types of Sudoku puzzles, from hard to evil. In this Sudoku tutorial, we'll explain how to identify W-Wings and share examples.

How to Find W-Wings

W-Wings are relatively easy to spot, making them a good technique to learn and practice if you're just beginning to improve your understanding of Sudoku strategies. However, they don't always lead to eliminations if the chain doesn't follow the logic described below.

Use these steps to help you find a W-wing in your Sudoku puzzle.

1. Identify two bi-value cells with the same candidates (x and y). These cells should not see each other, meaning that they are not in the same row, column, or block.
2. Find two more cells with a strongly linked conjugate pair of x or y. Each one of these linked cells should be visible to one of the bi-value cells. Remember, a strongly linked pair means that a specific candidate number only appears twice within a unit, so if one is false, then the other must be true.
3. Analyze the logic chain. The strongly linked pair is made of candidate x or y. In this example we'll use x. If x is true in one cell of the strongly linked pair, it must be false in the other cell of the strongly linked pair. Therefore, x can't be true in one of the bi-value cells, making one of the bi-value cells y, so any cell(s) that sees both bi-value cells cannot be Y.
4. Eliminate candidates. Because y must be true in one bi-value cell or the other, it cannot exist in any cells that see both bi-value cells. If it does, you can eliminate it as a candidate in those cells.

W-Wing Examples

Now that you have the general idea of how the technique is used, work through these examples with us to solidify your understanding.

W-Wing Example 1

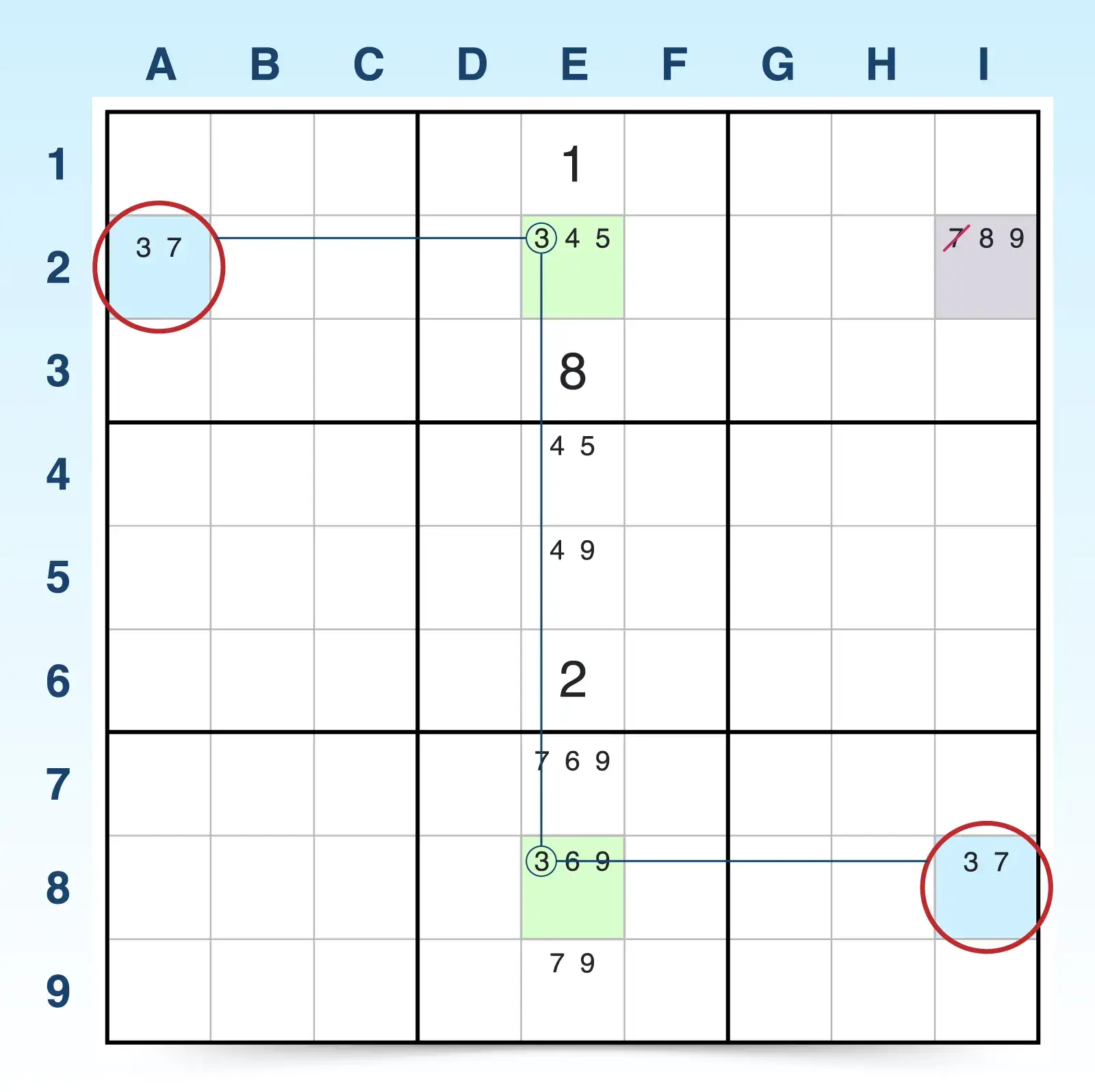
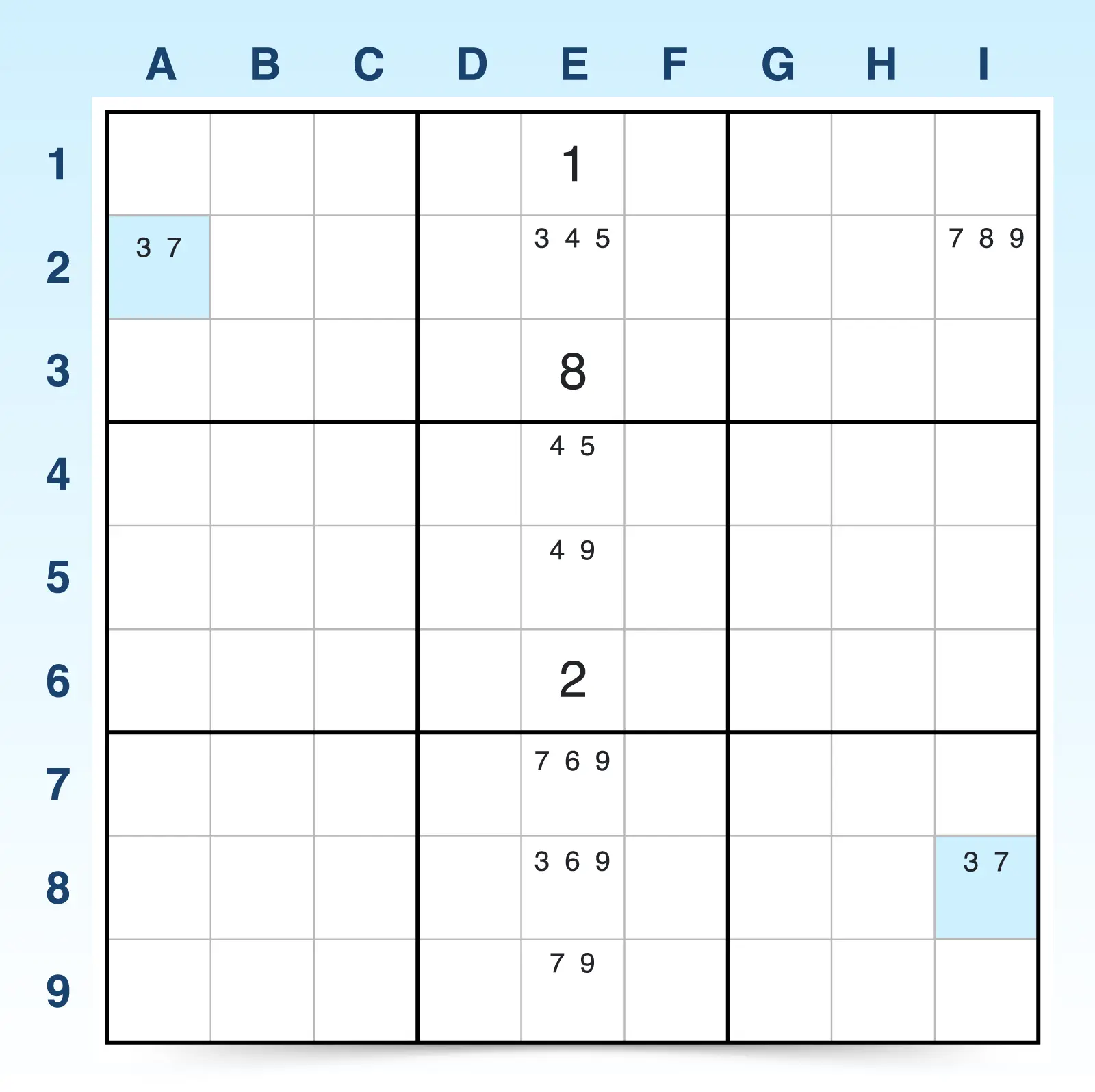
1. A2 and I8 both have identical bi-value candidates (3, 7) in cells that don't see each other.



2. Column E has a strongly linked conjugate pair of 3s in E2 and E8. E2 sees one of the bi-value cells (A2) and E8 sees the other bi-value cell (I8). This forms a linked chain.



3. Now you can use logic to determine if candidate elimination is possible.
• If E2 is 3, then E8 is not 3. Therefore A2 is 7.
• If E8 is 3, then E2 is not 3. Therefore I8 is 7.
• Either way, one bi-value cell must be 7.

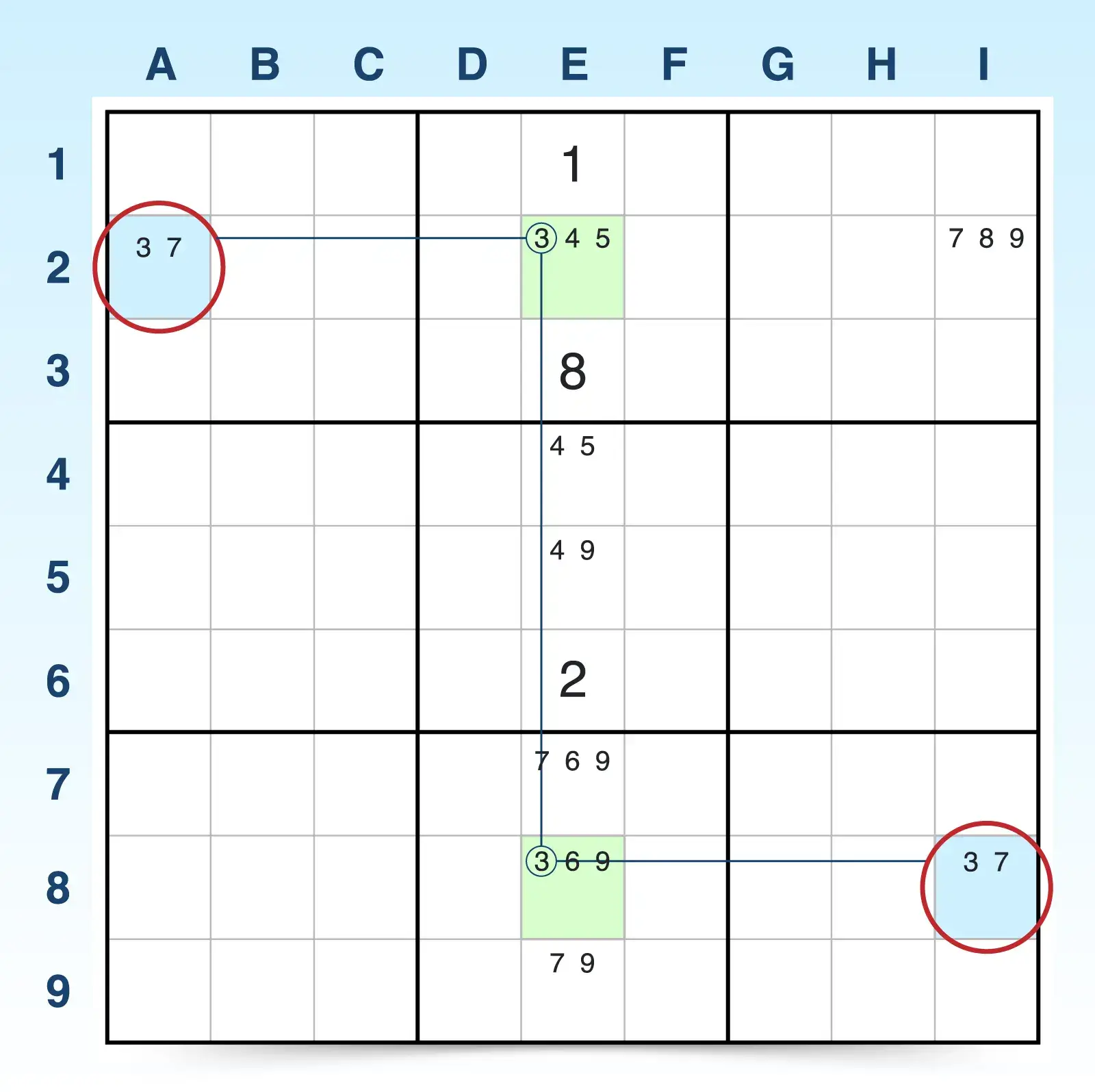
Because one bi-value must be 7, 7 candidates can be eliminated in any cells that see both bi-value cells. In this case, the 7 candidate can be eliminated in I2.

W-Wing Example 2

1. A5 and C8 both have identical bi-value candidates (2, 4) in cells that don't see each other.



2. The top left block has a strongly linked conjugate pair of 4s in B2 and C2. A2 sees one of the bi-value cells (A5) and C2 sees the other bi-value cell (C8).



3. The following logic confirms that elimination is possible.
• If A2 is 4, then C2 is not 4. Therefore A2 is 2.
• If C2 is 4, then A2 is not 4. Therefore C8 is 2.
• Either way, one bi-value cell must be 2.

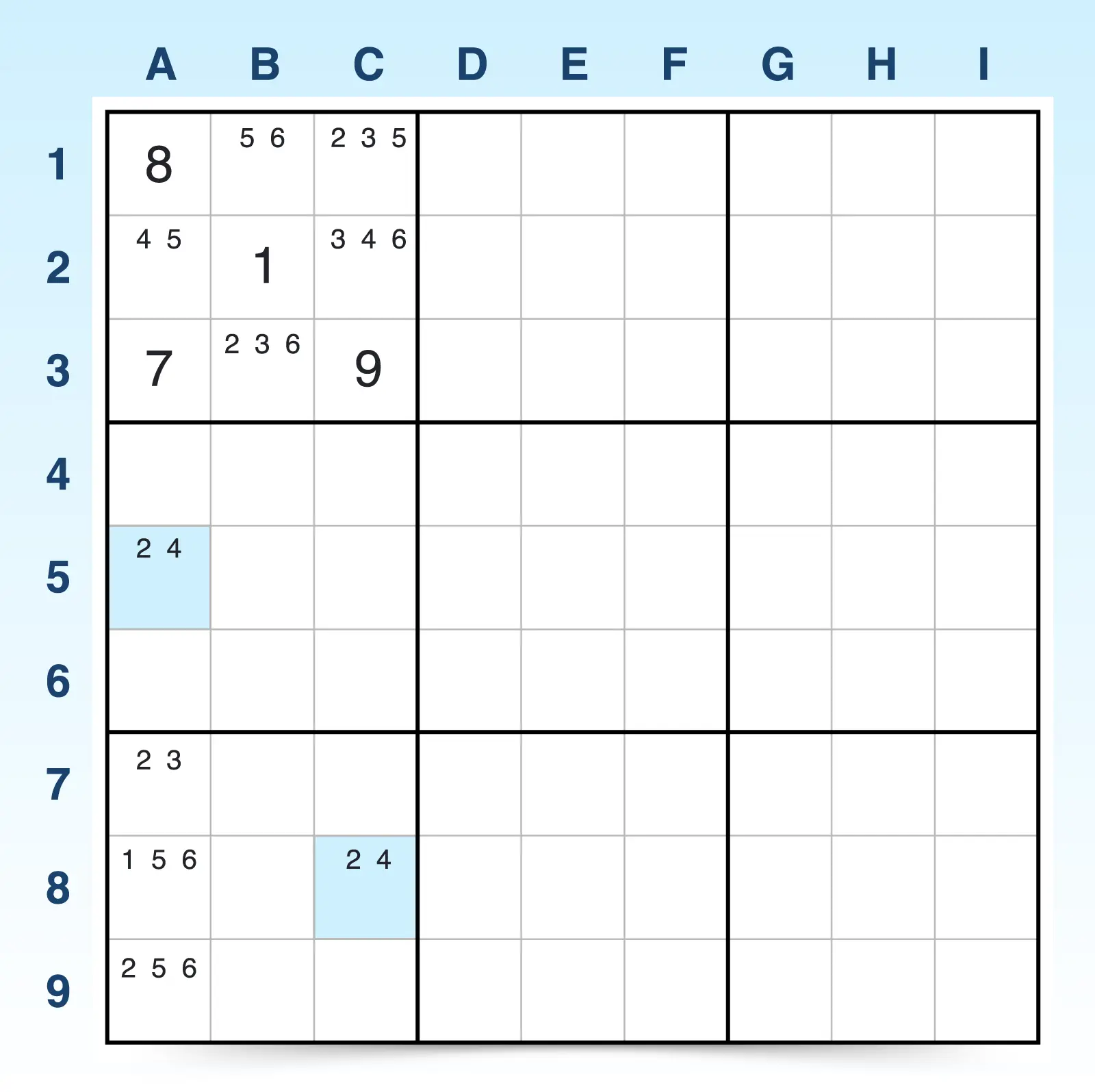
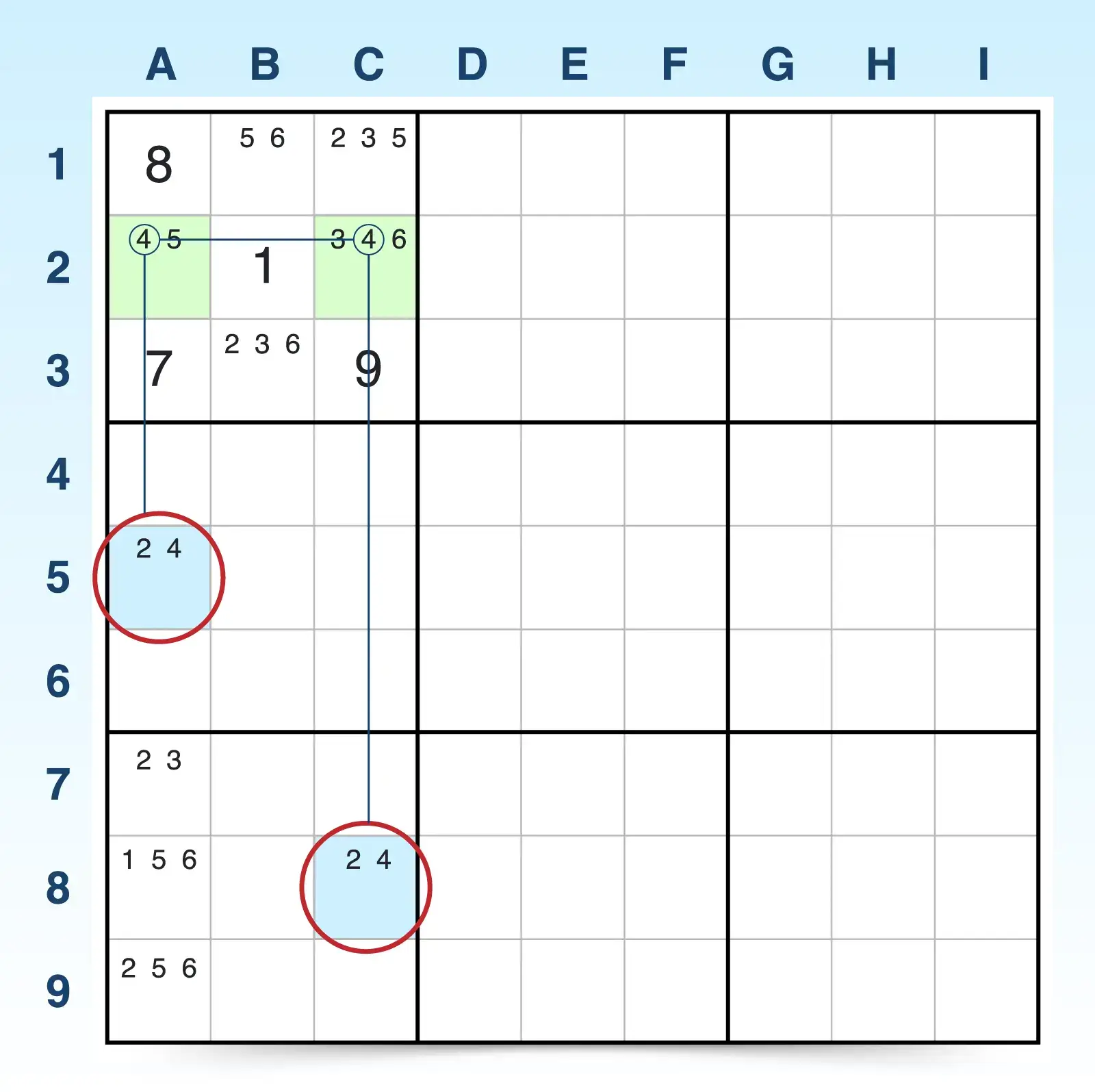
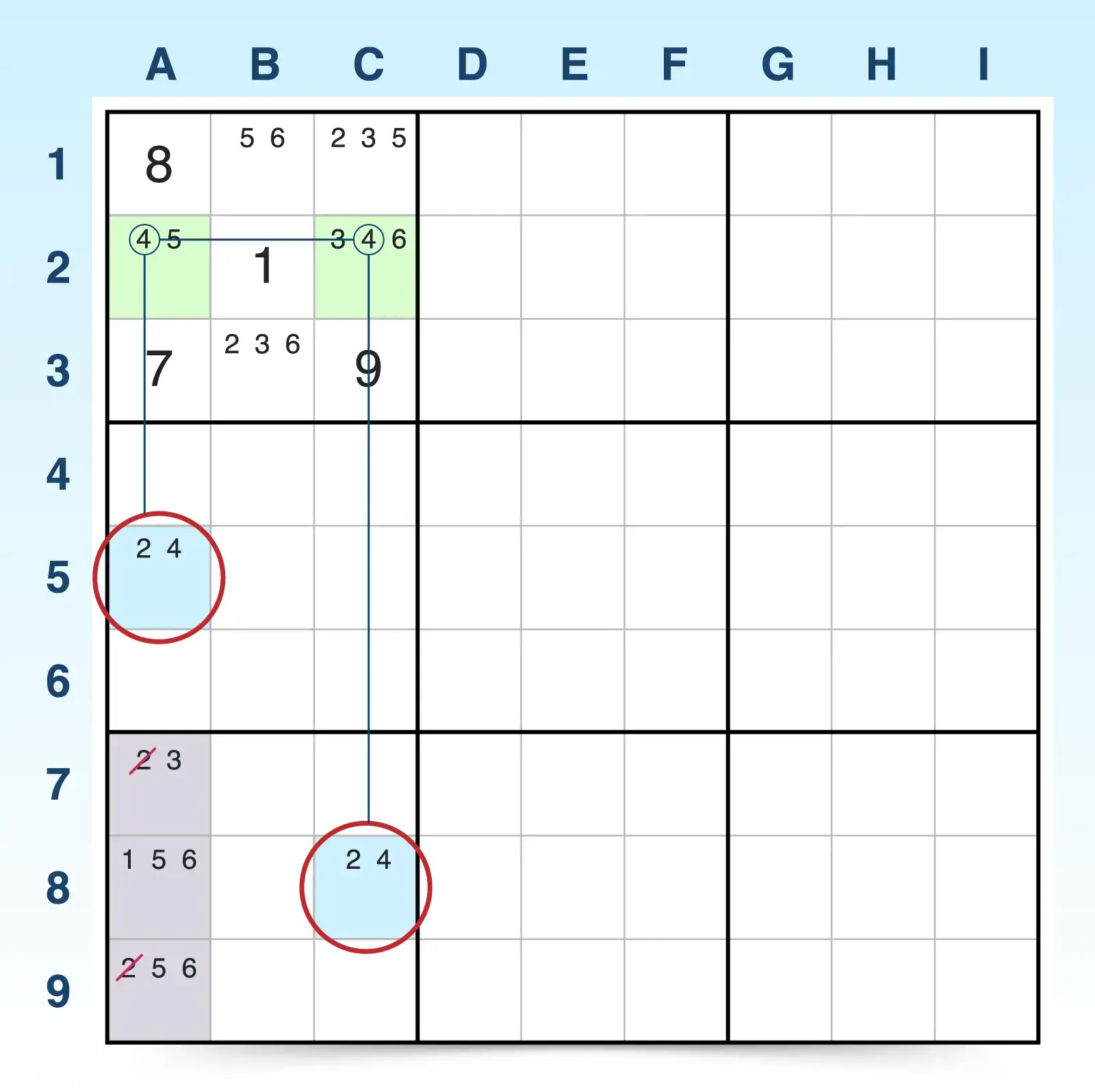
Because one bi-value cell must be 2, the 2 candidates can be eliminated in any cells that see both bi-value cells (A7, A8, and A9). Since there are 2s in A7 and A9, they can be eliminated.

Ready to see if you spot a W-Wing in a Sudoku puzzle? We offer hundreds of sudoku puzzles online for free!