Sudoku Simple Coloring Technique: Use Cases & Examples

Sudoku simple coloring, also known as single chains, is a single candidate strategy that focuses on identifying chains of conjugate pairs to make eliminations or solve cells.

A conjugate pair occurs when a candidate number appears in only two cells within a unit (row, column, or block). These two cells contain a strong link because if the candidate is the answer for one cell, it can’t be the answer for the other and vice versa.

In Sudoku coloring, you choose two different colors to represent the two possibilities for a candidate within a unit, understanding that each candidate is either the correct solution for a cell (true) or it isn’t (false). The dual-colored visualization helps you follow the logic in a chain and determine which color must be true based on the rules explained below.

To use the coloring technique, you start at the first conjugate pair and assign one cell a color (pink) and the other cell another color (blue). Then you create a chain of conjugate pairs for the same candidate, alternating colors for each connected cell. So if the blue cell has a strong link with another cell, that other cell will be pink.

Sudoku coloring also allows you to find contradictions. For example, if two cells of the same color appear in the same unit that means the same candidate would appears twice in the same unit, which breaks Sudoku’s uniqueness rule. Since this can’t happen, the color involved in the contradiction must be false, and the opposite color must be true.

The coloring Sudoku strategy is helpful for solving hard and expert Sudoku puzzles. Our tutorial will walk you through the basic rules and examples, so you can use this to find answers more quickly.

How to Find Sudoku Coloring Chains

Finding simple chains is as easy as identifying groups of conjugate pairs.

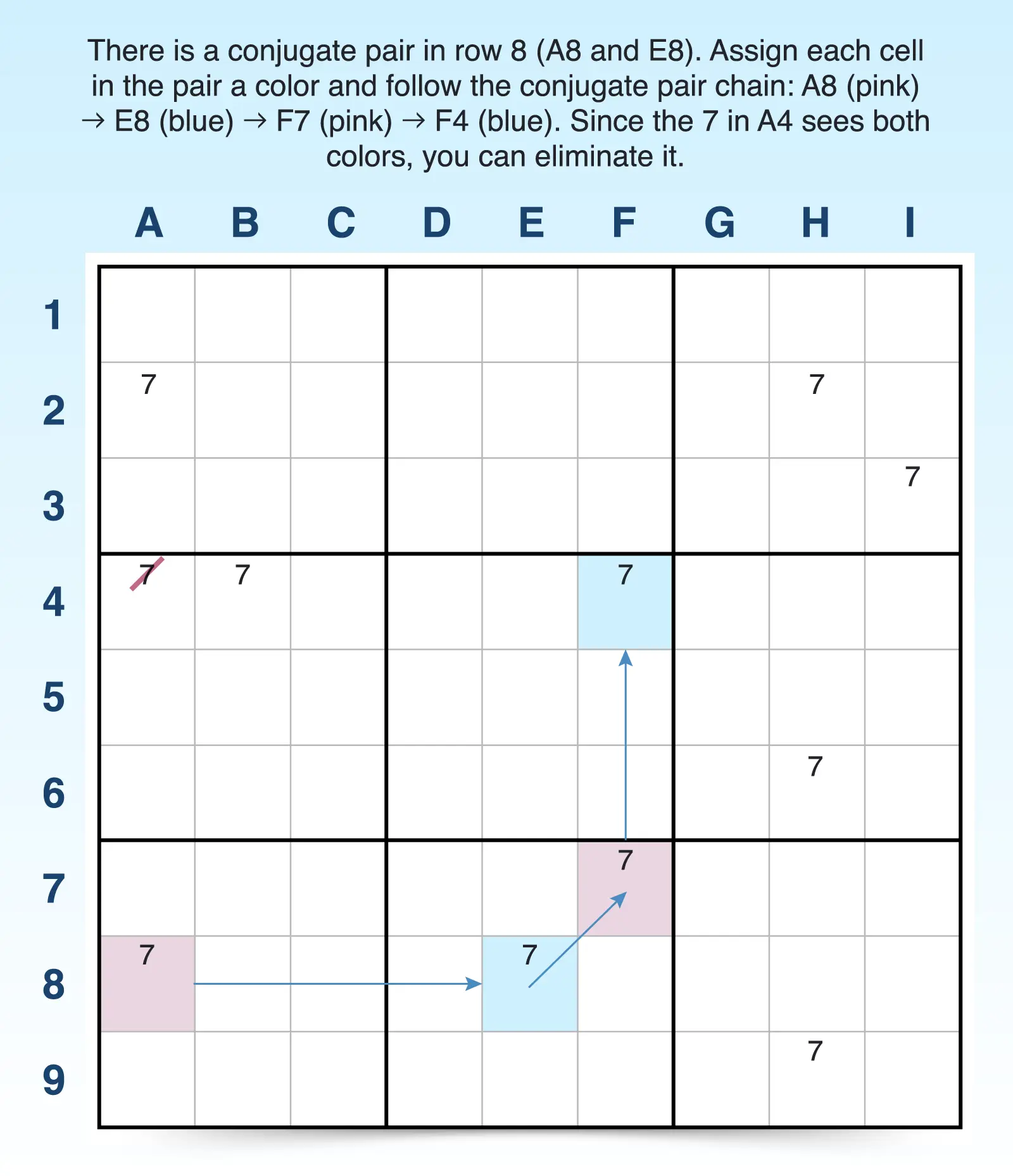
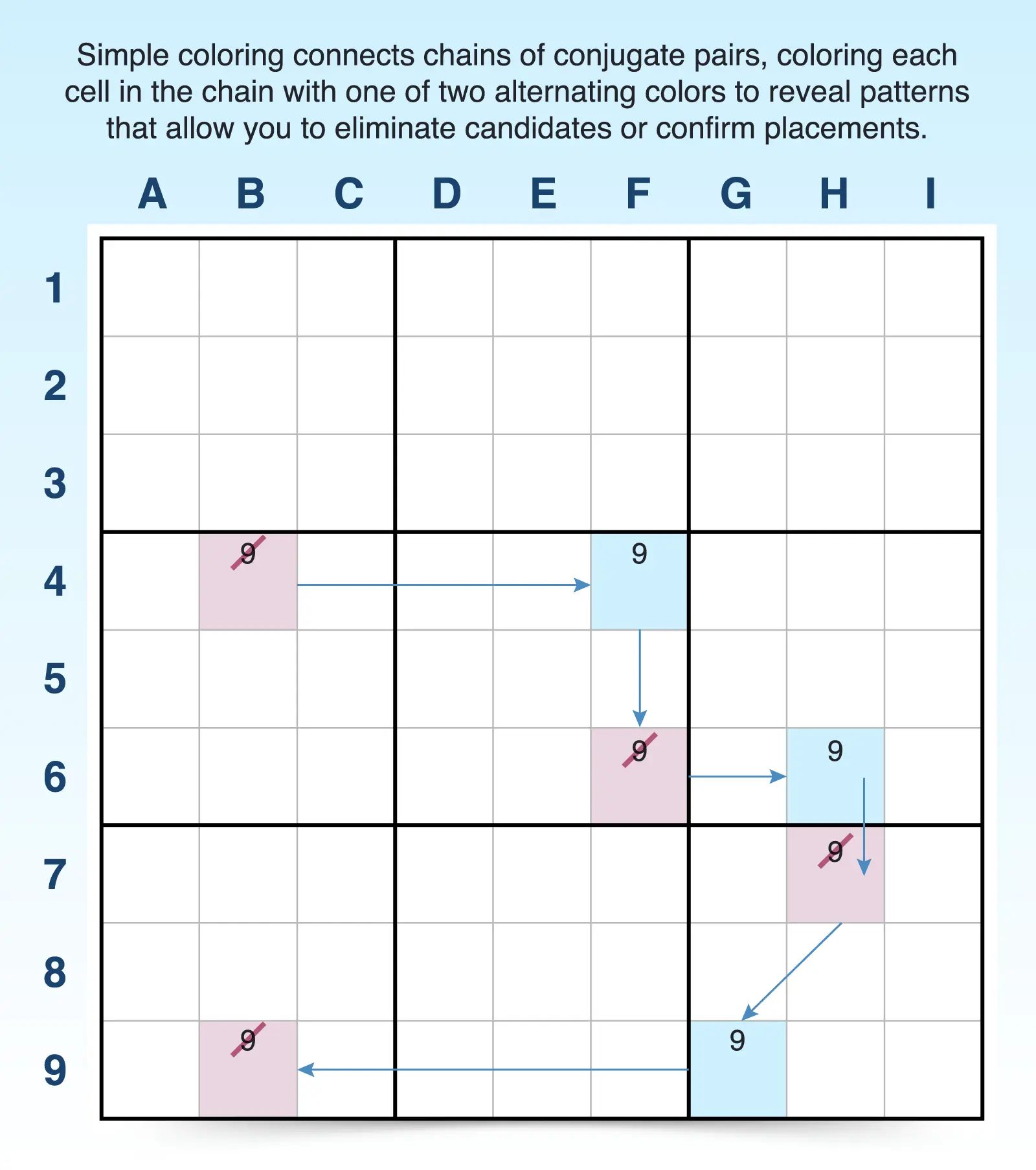
1. Find a conjugate pair. Remember, this is when a candidate only appears twice within a unit. For example, there are only two 7 candidates in row 8.
2. Choose two colors and assign each cell in the conjugate pair a different color. For example, the first cell in the conjugate pair (A8) is blue and the second (E8) is pink.
3. Look for another conjugate pair that links to the first conjugate pair and assign the new cell the opposite color. This happens when one of your colored cells shares a unit with another cell containing the same candidate, creating a new conjugate pair. For example, the 7 in F7 is the only other 7 candidate in the block, so it can be colored pink.
4. Repeat the process. Continue building the chain by following conjugate links and assigning alternating colors each time you connect to a new cell. In this case, you can color F4 blue, and that ends the chain.
5. Look for contradictions. Identify contradictions that can create eliminations. For example, if there are two of the same colors in a unit or a candidate outside the chain sees both colors, you can make eliminations. Since the 7 candidate in A4 sees both colors, you can eliminate it.

Sudoku Coloring Rules and Examples

There are two basic rules of simple chains, and cells can adhere to either or both of them. These rules help you find contradictions and make eliminations.

Rule 1 Example

Rule 1 focuses on eliminating the candidates of one color.

• Rule 1: If the same color appears more than once in a unit, the candidate cannot be the solution to those cells. Because each color represents a possible truth and Sudoku puzzles only have one right answer, two of the same candidates within a unit is impossible.
• Action: Eliminate the candidate in all cells with that color because the color represents a false option and look for cases where the opposite color is the solution.

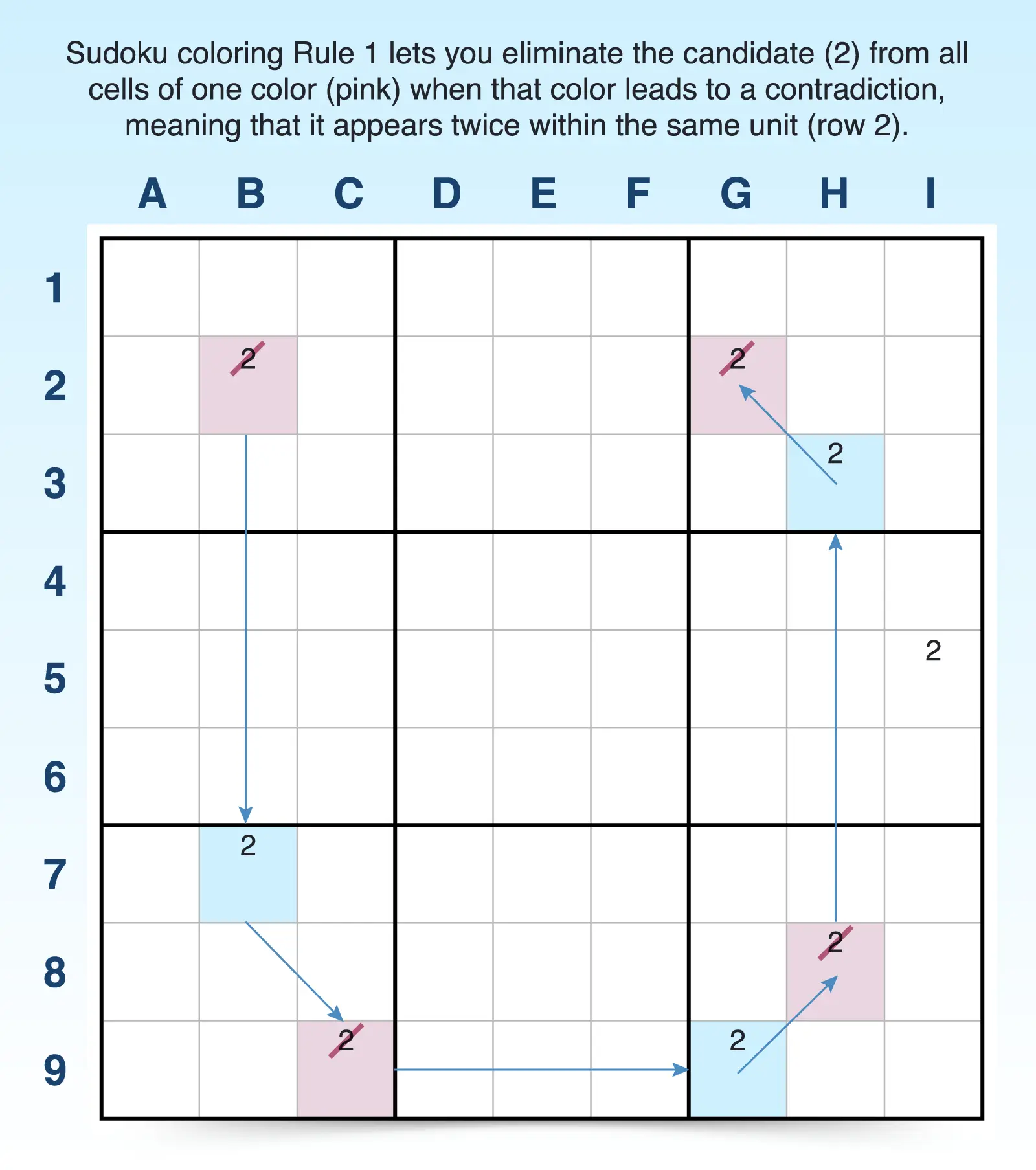
For example, you find a conjugate pair of 2s in column B (B2 and B7), so you color the first cell in the pair (B2) pink and color the second (B7) blue. You continue coloring linked conjugate pairs: C9 pink, G9 blue, H8 pink, H3 blue, G2 pink.

Once you reach the end of the chain, you notice that two cells in row 2 (B2 and G2) are both colored pink. This is impossible because the 2 candidate can’t be true for two cells within a row.

As a result, you can eliminate the 2 candidates from all pink cells and see if you can solve any of the blue cells or cells with other 2 candidates.

Rule 2 Example

Rule 2 focuses on eliminating candidates outside of the chain.

• Rule 2: If a candidate that is outside the coloring chain sees two cells of opposite colors, then one of those colored cells must be true, so the outside candidate cannot be the solution.
• Action: Eliminate the candidate from the uncolored cell, since it can't be true if it sees both colors.

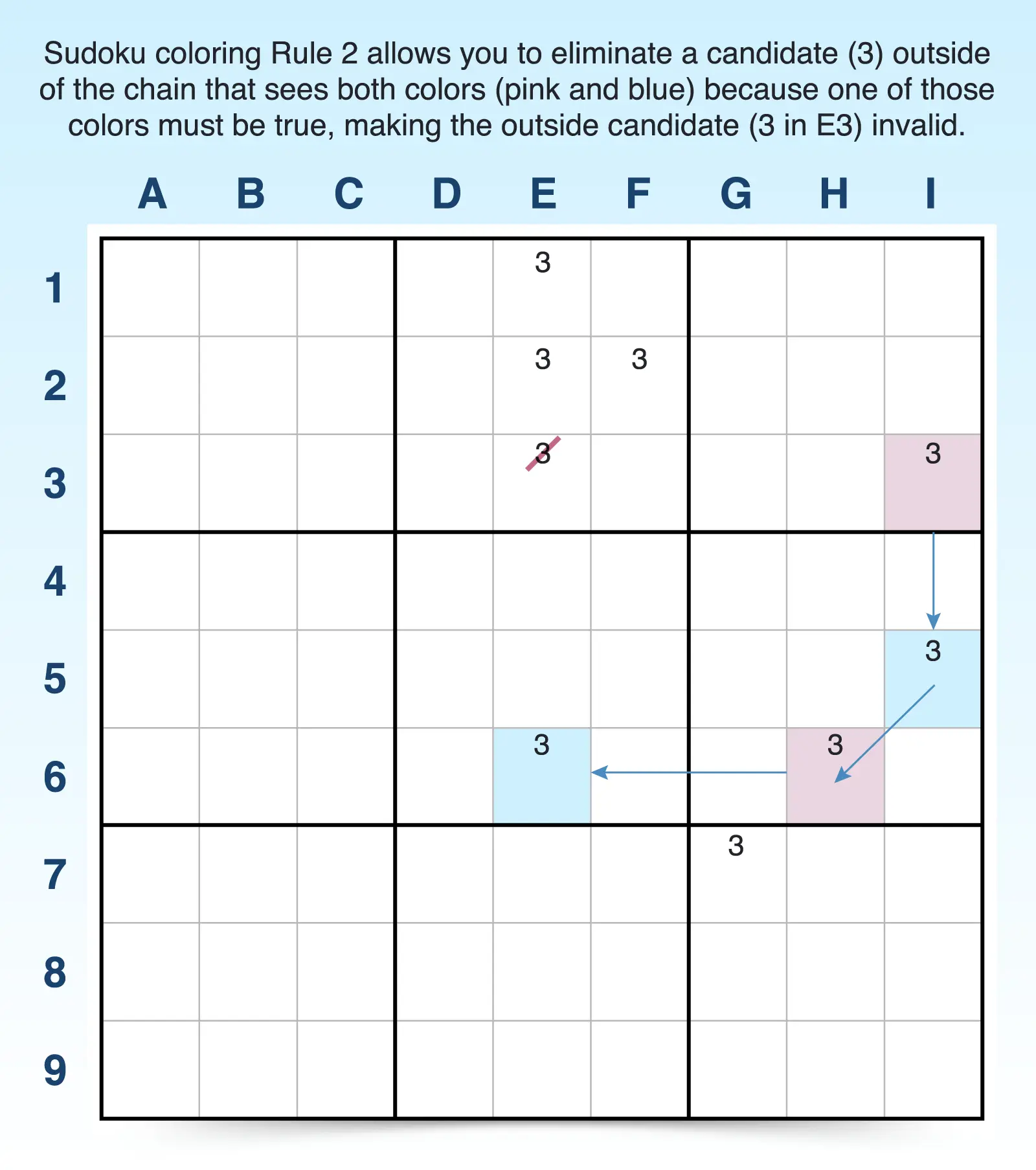
For example, you find a conjugate pair of 3s in column I (I3 and I5), so you color the first cell (I3) pink and the second cell (I5) blue. You continue coloring linked conjugate pairs: H6 pink and E6 blue.

Once you reach the end of the chain, you notice that the 3 candidate in E3 can see both colors (the blue E6 and the pink I3). Because of this, you can eliminate the 3 candidate in E3. The other 3 candidates such as E1 and G7 can’t be eliminated because they don’t see both pink and blue cells.

The coloring technique is a great way to visualize patterns and find eliminations on your Sudoku grid. If you want to continue to level up your Sudoku game, try other advanced strategies like X-wing or swordfish. We offer hundreds of free online Sudoku games and printables to test your skills.