Comment jouer au Sudoku Diabolique

Le Sudoku Diabolique est notre niveau de difficulté le plus élevé. Comme dans tout puzzle Sudoku, l'objectif est de compléter la grille 9x9 en remplissant les cases manquantes de sorte que chaque ligne, colonne et bloc 3x3 contiennent les chiffres de 1 à 9 une seule fois chacun.

Cependant, vous disposez de moins d'indices de départ, il vous faudra donc utiliser des stratégies avancées de Sudoku telles que X-wing, XYZ-wing, swordfish, chaînes de forçage et groupes presque verrouillés pour éliminer les candidats potentiels et déduire les réponses.

Stratégies pour le Sudoku Diabolique

Le niveau Diabolique demande de la patience et de la persévérance pour être résolu. Vous devrez utiliser des techniques avancées et une observation minutieuse pour remplir les cases et éliminer les candidats. Ces techniques de résolution du Sudoku, ainsi que celles présentées dans notre guide avancé de Sudoku, vous aideront à maîtriser les puzzles difficiles grâce à des stratégies Sudoku efficaces.

Chaînes de Forçage

La technique des chaînes de forçage utilise la logique « si, alors » en identifiant une case avec deux candidats et en modélisant quelle réaction en chaîne se produira si l’un ou l’autre des candidats est la bonne réponse. Ce faisant, vous trouverez des contradictions ou des confirmations, ce qui vous aidera à déterminer les réponses ou les exclusions.

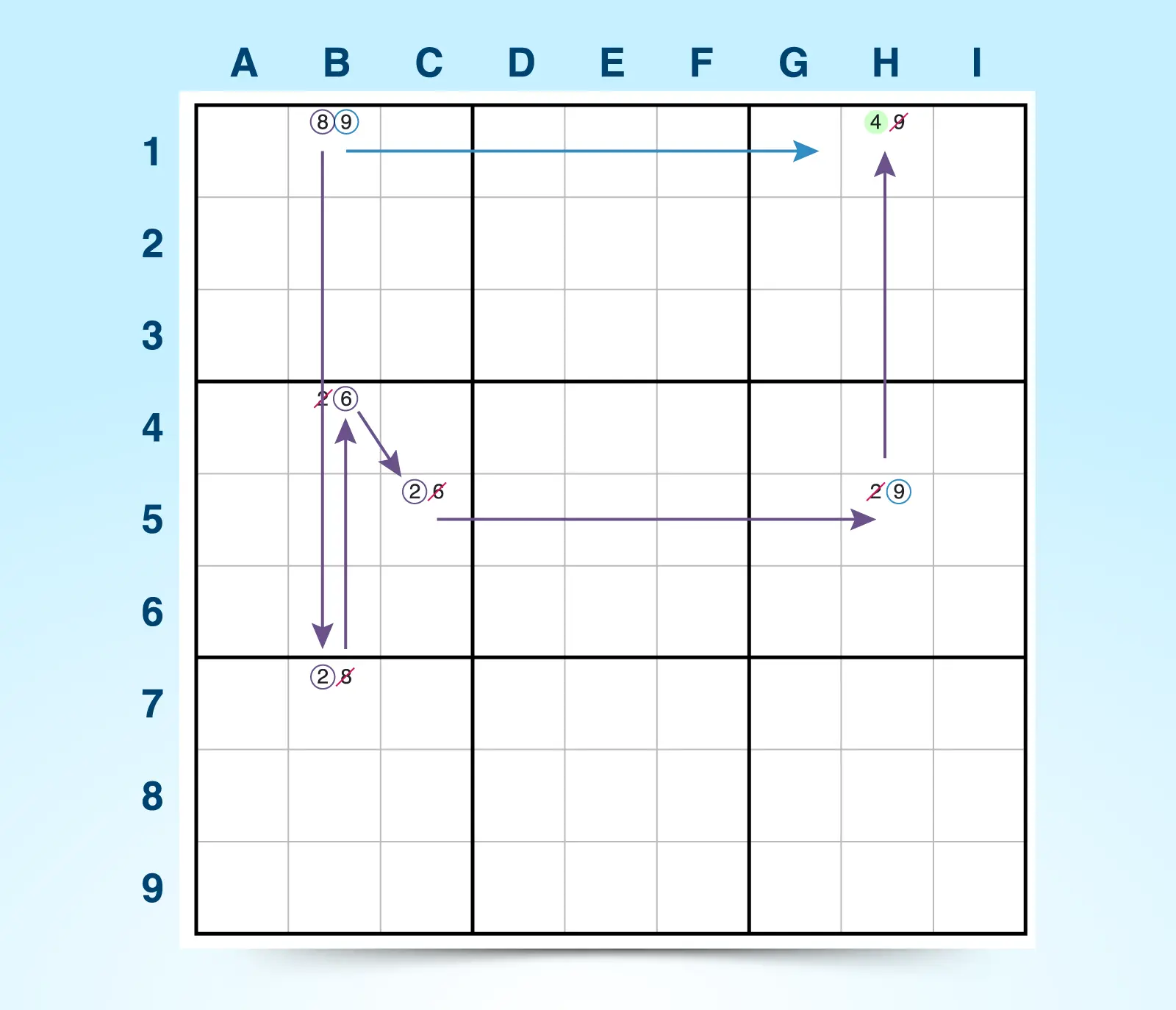
Cette solution n’est pas de la supposition car elle conduit à un résultat logique. Par exemple, dans le scénario ci-dessous, vous découvrirez que H1 a la même réponse, que B1 soit 8 ou 9. Cela confirme que H1 vaut 4.

Par exemple :

• Si B1 = 9, alors H1 = 4 et H5 = 9.
• Si B1 = 8, alors B7 = 2, B4 = 6, C5 = 2, H5 = 9, et H1 = 4.

Puisque la chaîne d’événements débutant à B1 confirme que H1 = 4 dans les deux scénarios, vous savez que 4 doit être la réponse pour H1.

Groupes Presque Verrouillés (ALS)

Un groupe verrouillé est un groupe de cases dans une unité où le nombre de candidats est égal au nombre de cases qu’ils occupent. Par exemple, si deux candidats potentiels sont confinés dans deux cases (aussi appelé paire nue), ce groupe de deux est un groupe verrouillé.

Un groupe presque verrouillé (ALS, pour « Almost Locked Set ») survient lorsque vous trouvez un groupe de cases dans une unité comprenant un candidat de plus que le nombre de cases. Par exemple, si trois candidats potentiels (1, 6, 7) sont répartis sur deux cases—(1, 6) dans une, et (6, 7) dans une autre—cela constitue un groupe presque verrouillé.

Lorsque deux groupes presque verrouillés partagent un candidat commun restreint, cela forme une chaîne continue au sein du groupe de cases, ce qui peut conduire à des éliminations. N'oubliez pas, pour qu’une paire de groupes presque verrouillés soit utile, ils doivent remplir les critères suivants :

• Toutes les cases de chaque groupe doivent pouvoir « se voir » (être sur la même ligne, colonne ou dans le même bloc) dans le groupe presque verrouillé.
• Il doit y avoir un candidat commun restreint, c’est-à-dire un candidat qui apparaît une fois dans les deux groupes presque verrouillés, mais qui ne peut être la réponse que pour un seul des groupes.
• Il doit y avoir un candidat commun présent dans les deux groupes, différent du candidat commun restreint.

Si tout cela est vrai, alors tout candidat de la grille qui peut « voir » tous les candidats communs des deux groupes ALS peut être éliminé.

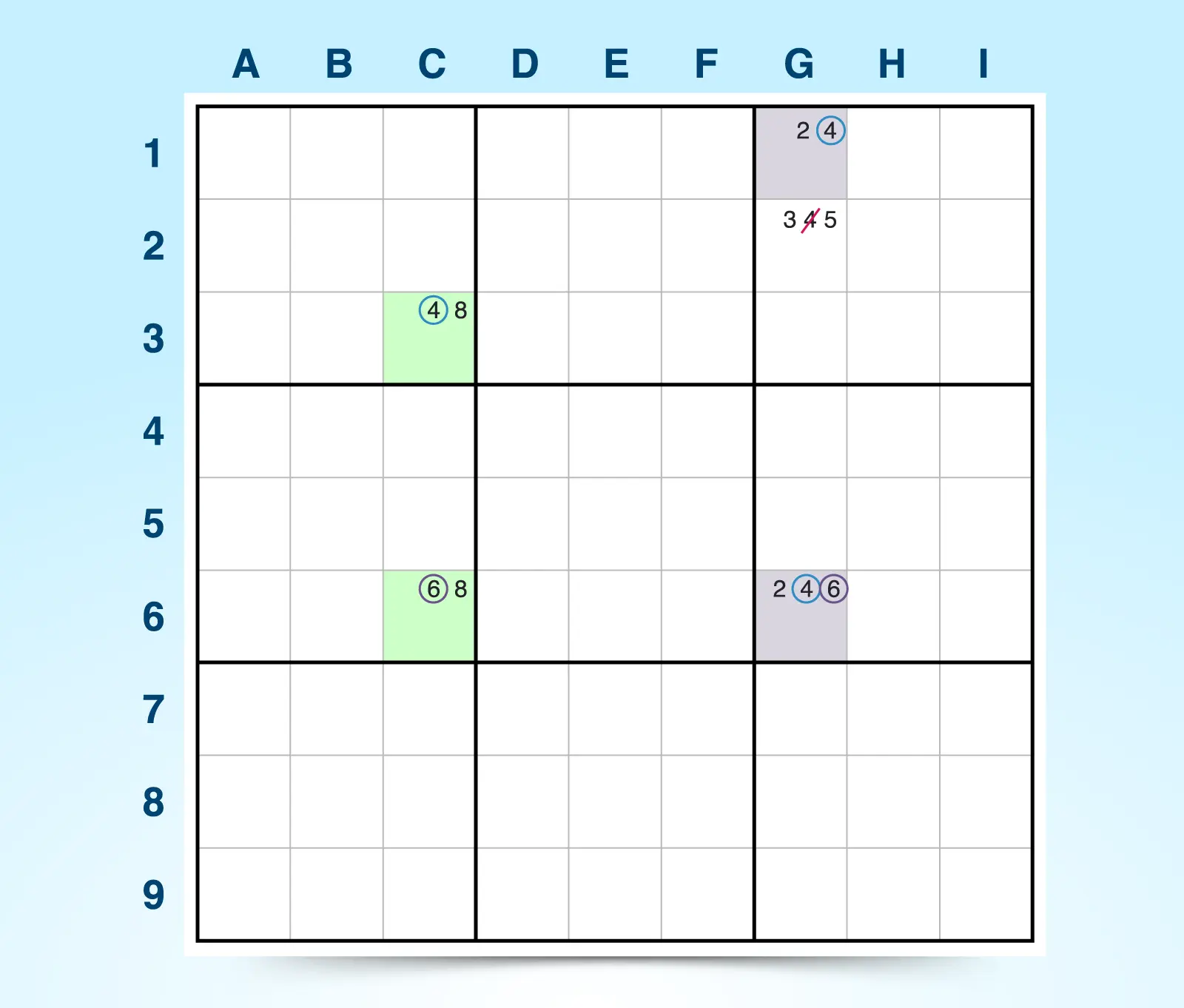
Dans l’exemple ci-dessous, C3 et C6 forment le premier groupe ALS et G1 et G6 constituent le second groupe ALS. Ils sont reliés par le candidat commun restreint 6, qui figure dans C6 et G6, mais ne peut être la réponse que pour l’un ou l’autre des groupes, jamais les deux. Les cases C3, G1 et G6 ont le candidat commun 4, donc tout candidat 4 en dehors des groupes ALS qui peut voir ces trois cases peut être éliminé. Ici, le candidat 4 en G3 est donc éliminé.

Nous proposons des grilles Sudoku pour tous les niveaux, du niveau Facile jusqu’au Sudoku Expert. De nouveaux jeux sont publiés chaque jour, et vous pouvez explorer notre archive pour des centaines de grilles imprimables ou en ligne afin de vous mettre au défi à tout moment, n’importe où !