Cum să joci Evil Sudoku

Evil Sudoku este cel mai dificil nivel al nostru. Ca la orice puzzle Sudoku, scopul este să completezi grila de 9x9 prin completarea numerelor lipsă astfel încât fiecare rând, coloană și bloc de 3x3 să conțină cifrele de la 1 la 9 exact o singură dată.

Totuși, vei avea mai puține cifre date, așa că va trebui să folosești strategii Sudoku avansate precum X-wing, XYZ-wing, swordfish, forcing chains și almost locked sets pentru a elimina candidații potențiali și a deduce răspunsurile.

Strategii pentru Evil Sudoku

Nivelul Evil necesită răbdare și perseverență pentru a fi rezolvat. Va trebui să folosești tehnici avansate și observație atentă pentru a completa celulele și a elimina candidații. Aceste tehnici de rezolvare Sudoku, precum și cele prezentate în ghidul nostru avansat Sudoku, te vor ajuta să stăpânești puzzle-urile provocatoare folosind strategii Sudoku eficiente.

Forcing Chains

Tehnica forcing chains folosește logica „dacă, atunci” prin identificarea unei celule cu doi candidați și modelarea reacției în lanț care va avea loc dacă unul dintre candidați este răspunsul sau dacă celălalt este răspunsul. Astfel, vei descoperi contradicții sau confirmări care te ajută să stabilești răspunsurile sau eliminările.

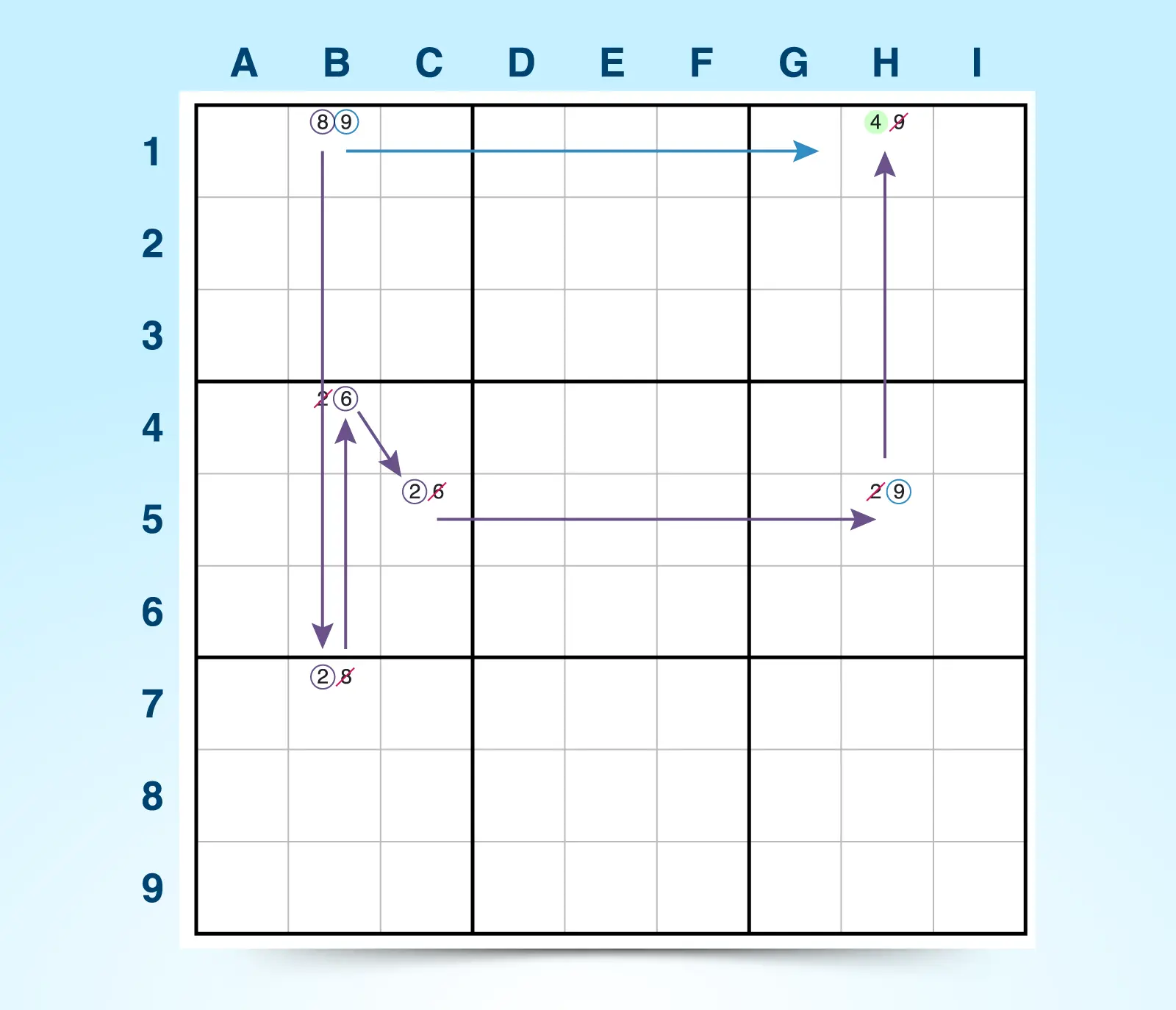
Această soluție nu este ghicită, deoarece te conduce la un rezultat logic. De exemplu, în scenariul de mai jos vei descoperi că H1 are același răspuns indiferent dacă B1 este 8 sau 9. Acest lucru confirmă că H1 este 4.

De exemplu:

• Dacă B1 = 9, atunci H1 = 4 și H5 = 9.
• Dacă B1 = 8, atunci B7 = 2, B4 = 6, C5 = 2, H5 = 9, iar H1 = 4.

Deoarece lanțul de evenimente pornind de la B1 confirmă că H1 = 4 în ambele scenarii, știi că 4 trebuie să fie răspunsul pentru H1.

Almost Locked Sets (ALS)

Un locked set este un grup de celule dintr-o unitate în care numărul candidaților se potrivește cu numărul de celule pe care le ocupă. De exemplu, dacă doi candidați potențiali sunt restrânși la două celule, cunoscut și ca naked pair, acest set de două este un locked set.

Un almost locked set (ALS) apare când găsești un grup de celule dintr-o unitate care conține un candidat în plus față de numărul de celule. De exemplu, dacă trei candidați potențiali (1, 6, 7) sunt distribuiți pe două celule—(1, 6) într-una și (6, 7) în cealaltă—aceasta formează un almost locked set.

Când două almost locked sets împart un candidat comun restricționat, se formează un lanț continuu în grupul de celule, ceea ce poate duce la eliminări. Amintește-ți, pentru ca o pereche de almost locked sets să fie utilă, trebuie să îndeplinească următoarele criterii:

• Toate celulele din fiecare set trebuie să poată „vedea” (să fie în același rând, coloană sau careu) o altă celulă din almost locked set.
• Trebuie să existe un candidat comun restricționat, adică un candidat care apare în ambele almost locked sets o singură dată, dar poate fi răspunsul doar pentru unul dintre seturi.
• Trebuie să existe un candidat comun prezent în ambele seturi, care nu este candidatul comun restricționat.

Dacă toate acestea sunt adevărate, atunci orice candidat din grilă care poate „vedea” toți candidații comuni din ambele grupuri ALS poate fi eliminat.

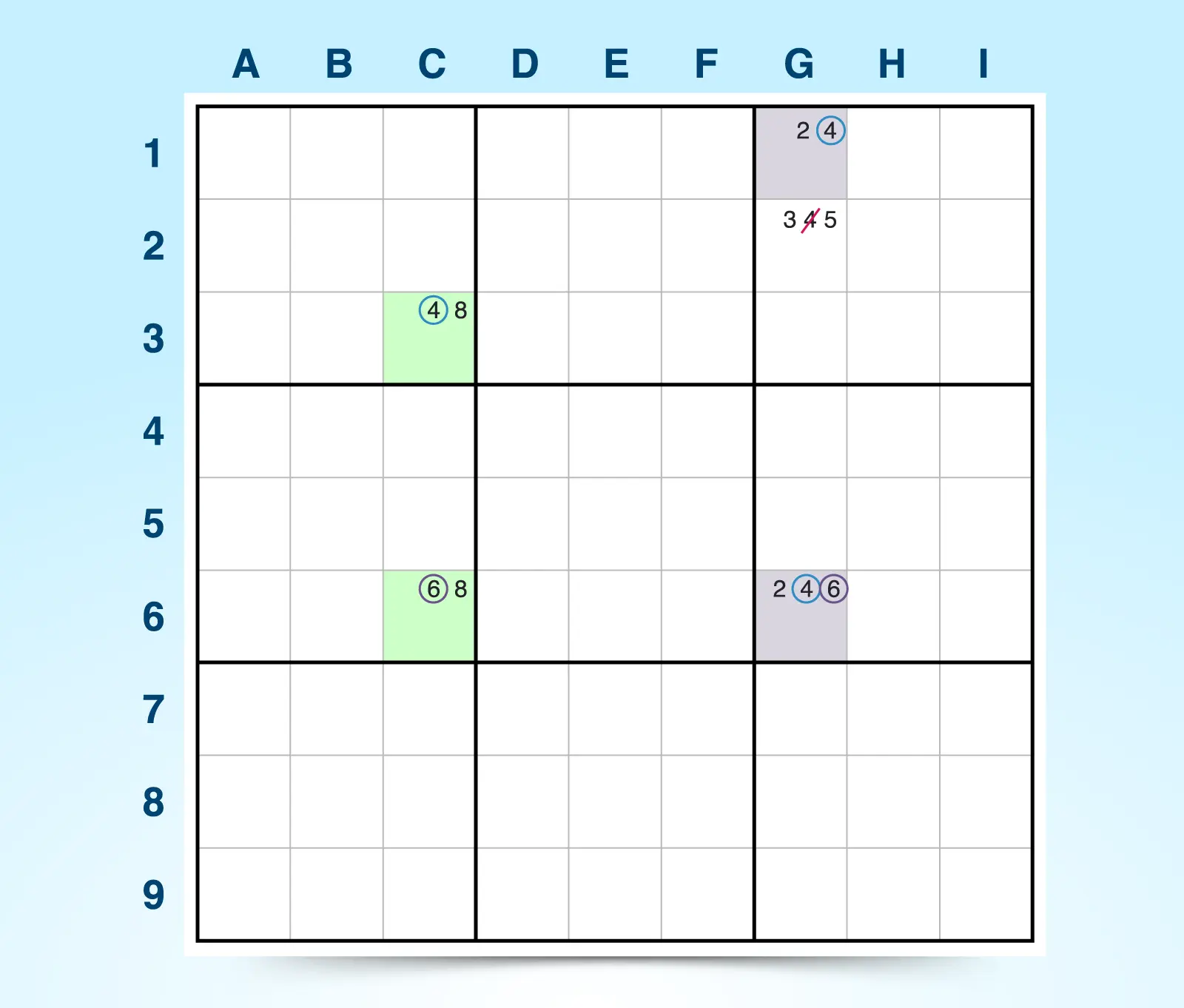
În exemplul de mai jos, C3 și C6 formează primul ALS, iar G1 și G6 formează al doilea ALS. Ele sunt conectate de candidatul comun restricționat 6, care apare în C6 și G6, dar poate fi răspunsul doar pentru unul dintre ALS, nu pentru ambele. Celulele C3, G1 și G6 au candidatul comun 4, așa că orice candidat 4 din afara grupurilor ALS, care poate vedea cele trei celule, poate fi eliminat. În acest caz, candidatul 4 din G3 este eliminat.

Oferim puzzle-uri Sudoku pentru toate nivelurile de experiență, de la Nivel ușor până la Sudoku expert. Publicăm jocuri noi în fiecare zi și poți explora arhiva noastră pentru sute de puzzle-uri printabile și online pentru a te provoca oricând și oriunde!