Last Possible Candidate Technique: Use Cases & Examples

The last possible candidate strategy is a basic Sudoku solving technique that helps you find the only number that can fit into a cell by eliminating possibilities from its row, column, and 3x3 block. When one number is missing from all three units and all other numbers are accounted for at least once, the missing number has to be the answer for the cell.

Although many beginners use this technique, all Sudoku solvers rely on this fundamental strategy to clean up obvious placements. And the logic of this strategy underpins other patterns, such as naked singles, hidden singles, and locked candidates as well as more advanced strategies. So mastering this technique can help you not only solve more Sudoku puzzles but also allow you to level up when you play Sudoku online.

How to Find the Last Possible Candidate

To use the last possible candidate Sudoku strategy, you compare a cell’s relationship with each unit and make conclusions about what numbers (or candidates) might be placed in that cell. In a Sudoku grid, every unit (row, column, and 3x3 block) must have the numbers 1 through 9 placed in them only once. For example, if you’re trying to figure out whether a 5 can go into a particular cell in a row, you know the 5 cannot be placed in that cell if the same row has a 5 in it already.

last possible candidate example

To find the last possible candidate number for a unit, follow these steps:

1. Select a Target Cell

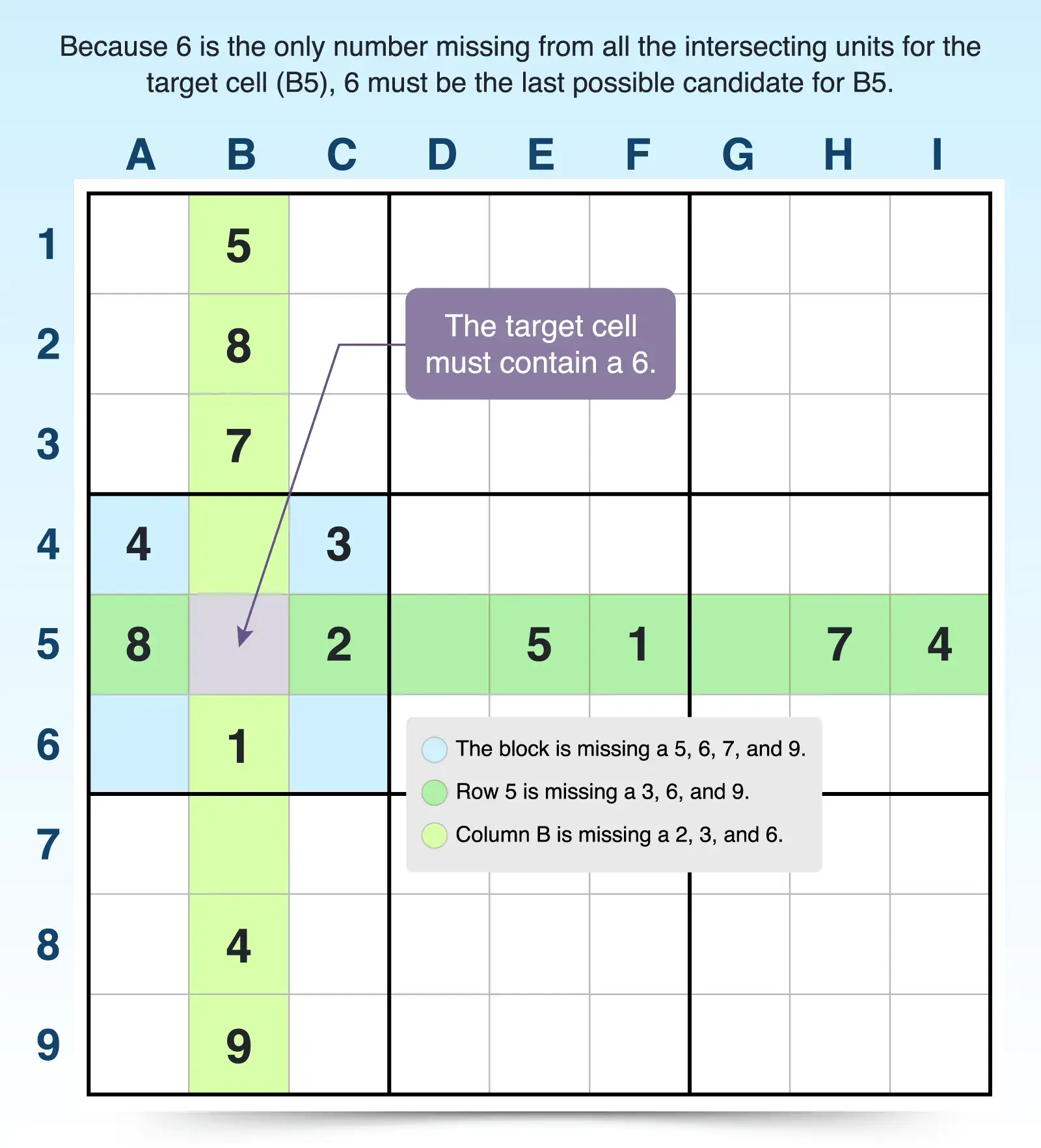
You can select any empty cell in any row, column, or 3x3 block to target. For beginners, it’s easiest to start with a cell that has a lot of answers in its three intersecting units. For this example, cell B5 has a lot of answers in its row (5) and column (B), making it a good choice for this strategy.

A target cell doesn’t have to be the only cell left in a unit. Even if a unit has several empty cells, you may still be able to determine the last possible number if the attached units have a lot of answers in them already.

2. List the Givens and Answers in Each Unit

Identifying the givens (numbers already in the grid) and the answers (placements you’ve made) helps narrow down the possible candidates for a cell. Any number already present in the row, column, or 3x3 block cannot go in the target cell.

For example, the following numbers are already placed in the units for cell B5, so they can’t be the answer to your target cell:

  • Row 5: 1, 2, 4, 5, 7, and 8
  • Column B: 1, 4, 5, 7, 8 and 9
  • 3x3 block (columns A through C and rows 4 through 6): 1, 2, 3, 4, and 8

3. Identify the Missing Numbers in Each Unit

Since a cell cannot repeat numbers from any unit, focus on which numbers are missing from its row, column, and block. By comparing the missing numbers to the present numbers across the three units, you can conclude the following:

  • If you find that a number is missing in one unit but is present in another, then you know that candidate cannot be the answer to your target cell. This eliminates it as a possibility.
  • If you find only one number missing in every unit, that number is your last possible candidate for your target cell.
  • If more than one number is missing from all units, you can’t confirm the last possible candidate, but you can narrow down the candidates for the cell, which is useful for other basic techniques when solving.

In this example, the missing numbers include:

  • Row 5: 3, 6, and 9
  • Column B: 2, 3, and 6
  • 3x3 block: 5, 6, 7, and 9

Only one number, the number 6, is missing from all units. That means a 6 must be placed into B5 for each of its units to have 1 through 9 placed in them with no repeats.

You can see this by comparing the givens and missing numbers across the intersecting units. Although row 5 is missing 3, 6, and 9, column B contains a 9, which narrows the possible candidates down to just 3 and 6. However, because the 3x3 block has a 3 placed in it, 3 cannot be a candidate, which means the last possible candidate for cell B5 is 6.

With practice, you’ll be able to mentally count from 1 to 9 and cross off the numbers already in the intersecting units, making it easy to spot the last possible candidate.

Remember: You won’t always find the last possible candidate, especially as you level up to more difficult Sudoku puzzles. But this process still gives you an advantage. By comparing missing numbers to the givens and answers in each unit, you can narrow down candidates, add pencil marks, and build a foundation for many other Sudoku strategies.

Last Possible Candidate Examples

You can target any cell to try to find its last possible number, but the key is to target a cell that belongs to at least one unit with a lot of givens or answers already, especially if you’re a beginner. You can use this Sudoku technique at any stage of your puzzle solving.

Last Possible Number for a Row Example

To find the last possible number for a row, follow these steps:

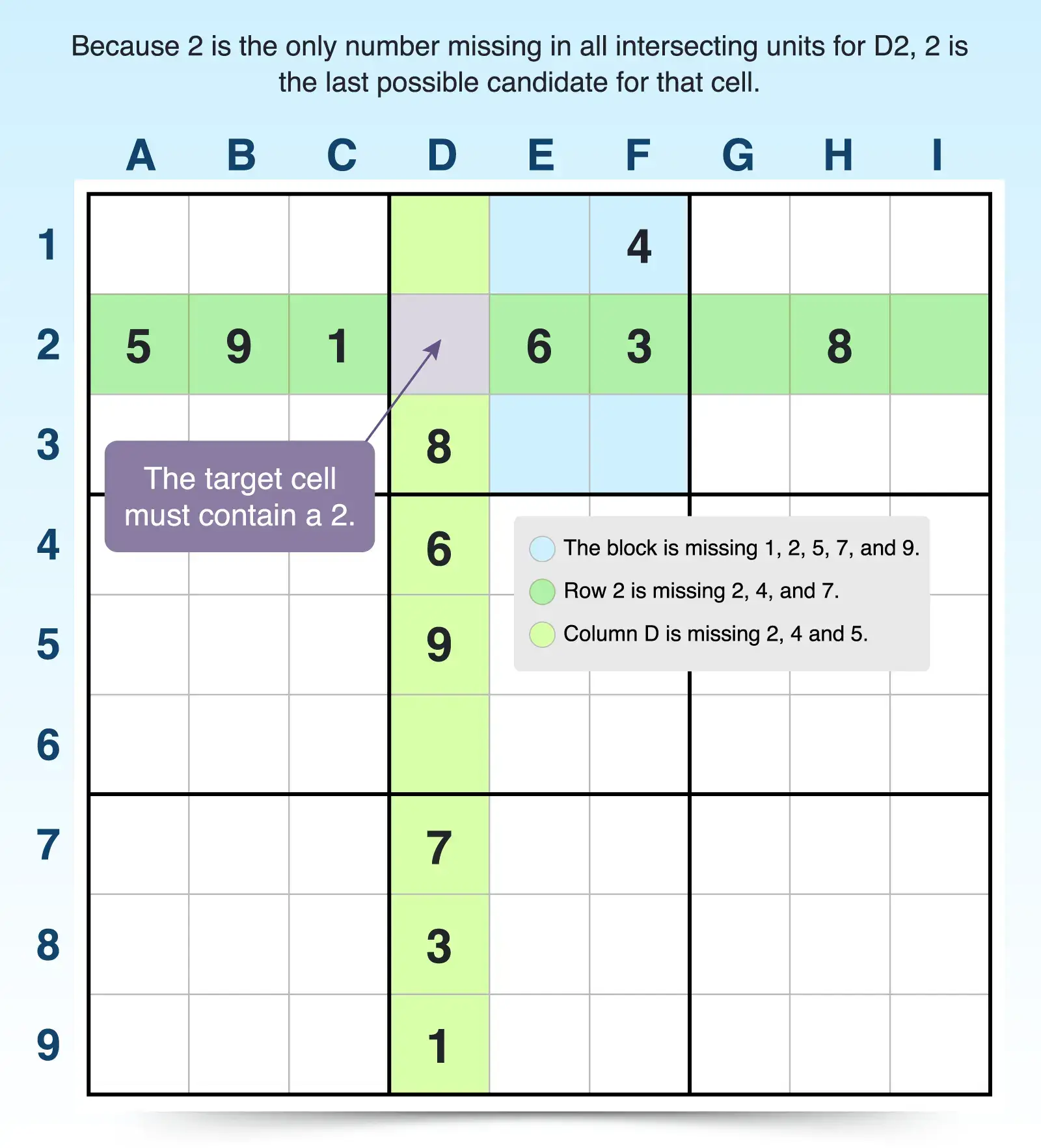
last possible candidate row example
  1. Select an empty cell in one row to target. Typically, targeting a cell with a lot of givens in its intersecting units is easier to start with. For example, cell D2 is a good choice because row 2 and column D have many givens.
  2. List the givens in each unit. For example, row 2 has numbers 1, 3, 5, 6, 8, and 9; column D has a 1, 3, 6, 7 8, and 9; and the 3x3 block (rows 1 through 3 of columns D through F) has 3, 4, 6, and 8.
  3. Identify the missing numbers in each unit. The missing numbers for row 2 include 2, 4, and 7. Column D is missing 2, 4, and 5; and the block is missing numbers 1, 2, 5, 7, and 9. Because 2 is missing in all units, 2 is the last possible candidate and must be placed into D2.

Last Possible Number for a Column Example

last possible candidate column example

To find the last possible candidate for a column, follow these steps:

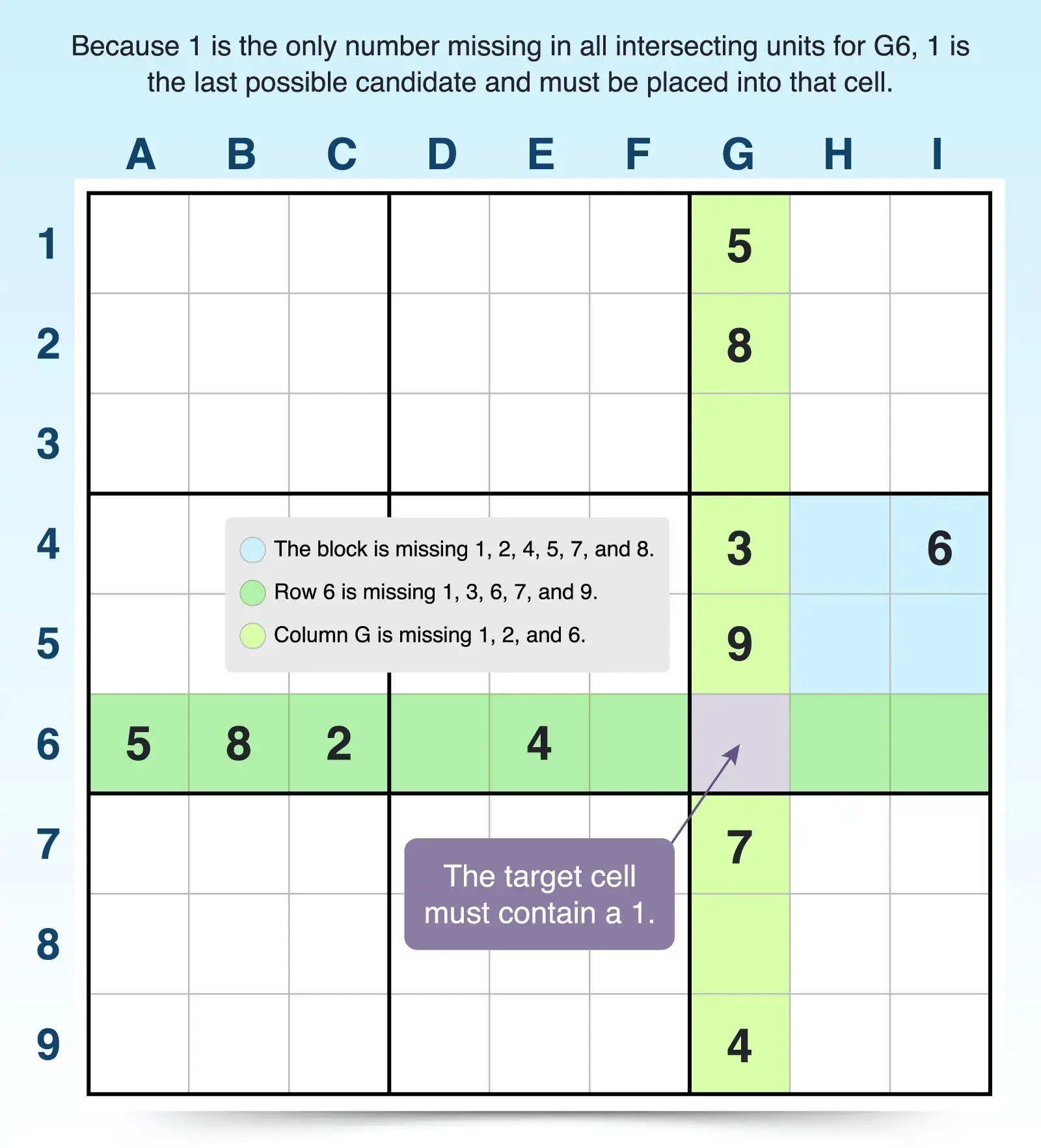
  1. Select a target cell in a column. Try looking for one that already has a lot of answers or givens in its units. For example, the units associated with G6 have a lot of givens.
  2. List the givens in each unit. For example, column G has numbers 3, 4, 5, 7, 8, and 9, and row 6 has 2, 4, 5, and 8. The 3x3 block (with rows 4 through 6 of columns G through I) has numbers 3, 6, and 9.
  3. Identify the missing numbers in each unit. For example, column G is missing 1, 2, and 6, and row 6 is missing 1, 3, 6, 7, and 9. And the block is missing 1, 2, 4, 5, 7, and 8. Candidate 1 is missing from all units, and that means that the last possible candidate for G6 must be 1.

Last Possible Number for a Block Example

To find the last possible candidate for a block, follow these steps:

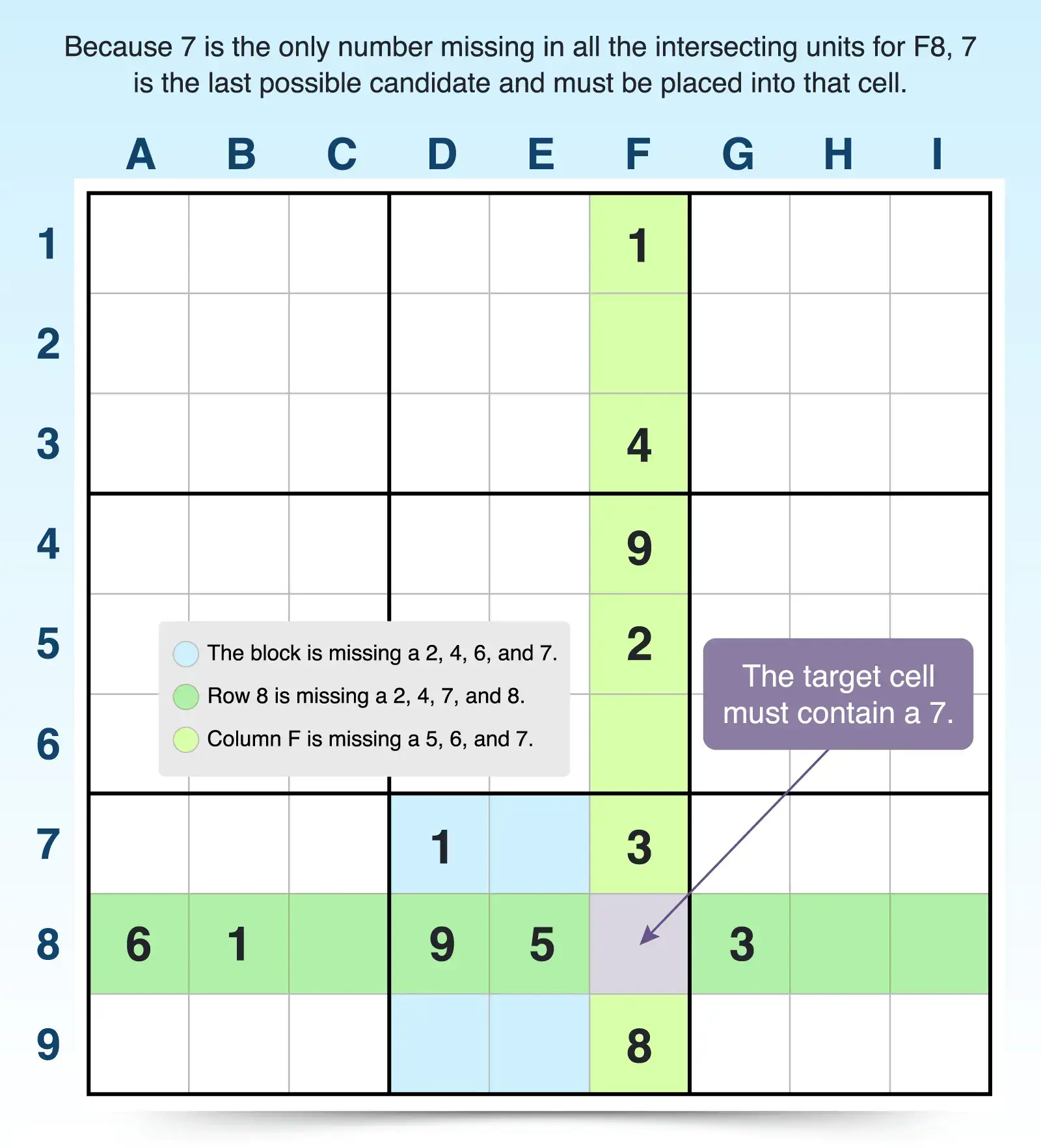
last possible candidate block example
  1. Select a target cell in a block. Although it’s helpful to find a cell within a block that already has a lot of givens, you can also look for a cell with a lot of answers in its related row and column. For example, cell F8 has a lot of givens in the block (rows 7 through 9 and columns D through F), and it also has several answers in its related units (row 8 and column F).
  2. List the givens in each unit. For example, the block already has numbers 1, 3, 5, 8 and 9. Row 8 has a 1, 3, 5, 6, 8, and 9, and column F has a 1, 2, 3, 4, 8, and 9.
  3. Identify the missing numbers in each unit. For example, this block is missing 2, 4, 6, and 7. Row 8 is missing 2, 4, 7, and 8, and column F is missing 5, 6, and 7. Because candidate 7 is missing from all units related to F8, 7 is the last possible candidate for that cell.

While advanced techniques like X-wing, swordfish, or XY-wing may be necessary for hard Sudoku puzzles, starting with the last possible candidate technique lays a solid foundation for solving Sudoku puzzles.

Whether you’re tackling an easy Sudoku puzzle or get stumped on a hard one, applying the last possible candidate technique leverages the givens and pencil marks in a puzzle to discover a single candidate that breaks the gridlock.