The Phistomefel ring, also referred to as Phistomefel’s theorem, states that the four sets of 2x2 cells in each corner of the puzzle must contain the same 16 digits as the ring of 16 cells that surrounds the center 3x3 block. This Sudoku strategy, introduced by the puzzle creator who goes by the pseudonym “Phistomefel,” allows you to narrow down placements in those cells and eliminate candidates as you work through the puzzle.

When you find yourself getting stuck with other Sudoku techniques, Phistomefel ring can help break open your puzzle and reveal new placements when you play Sudoku online.

Understanding Set Equivalence Theory

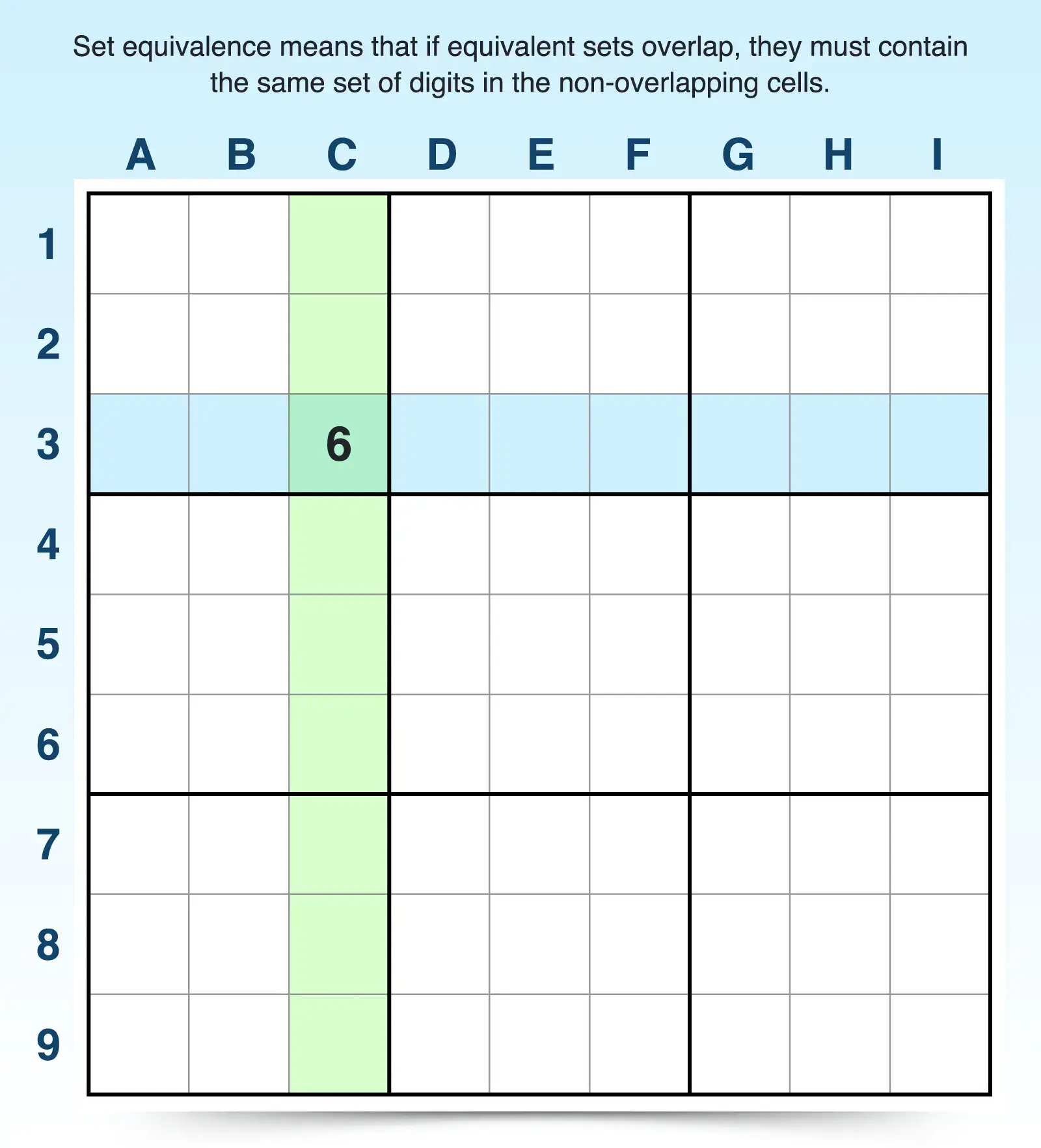
Set equivalence in Sudoku means that when equivalent units overlap, the cells outside the overlap must contain the same remaining numbers.

For example, because each unit must include the digits 1 through 9 exactly once, when one unit overlaps with another unit (like a row overlapping a column), their overlapping cell is a shared digit and all the non-overlapping cells must contain the same set of digits (an equivalent set).

More specifically, row 3 and column C overlap at one cell, C3. Because that row and column can only contain digits 1 through 9 and none can repeat, cell C3 must have only one answer. In this case C3 is 6. That means two sets of the same numbers—1, 2, 3, 4, 5, 7, 8, and 9—must appear somewhere in both row 3 and column C.

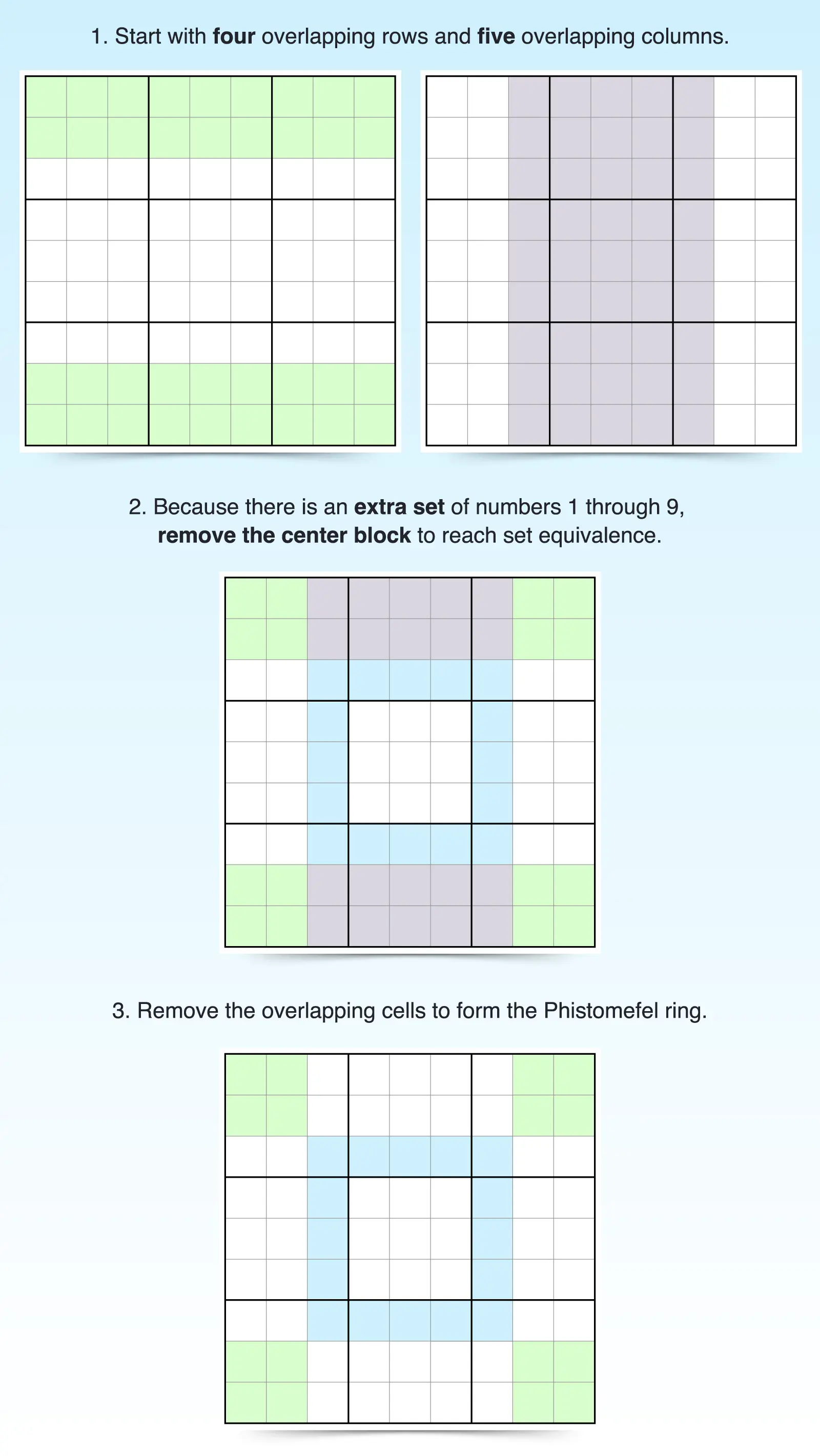
How Phistomefel Ring Works

To use the Phistomefel ring technique, you must make sure that the quantity of a particular candidate’s appearance in the corners of the puzzle matches the quantity of its appearance in the ring and vice versa. The four 2x2 boxes in each corner (shaded in green) must contain the same set of digits as the ring of 16 cells that border the center block (shaded in blue). By understanding how this works, you can use it to your advantage when solving Sudoku puzzles.

Phistomefel ring relies on the fact that overlapping units must have equivalent sets of numbers to create the ring technique. Consider how the overlapping impacts candidate placement by examining the reasoning behind the theorem:

Identify the sets.
• Rows 1, 2, 8, and 9: These 36 shaded cells (green) must contain 1 through 9 exactly four times (once per row).
• Columns C, D, E, and G: These 45 shaded cells (light purple) must contain 1 through 9 exactly five times (once per column).
Create set equivalence.
• Because there are 45 column cells but only 36 row cells, the columns have one extra set of numbers meaning they don’t have set equivalence.
• To create equivalence, you must remove one set (the center 3x3 block).
Form the ring.
• Remove overlapping cells (light purple).
The non-overlapping cells must contain the same set of digits, which creates
• Phistomefel’s ring (light blue).

Phistomefel Ring Example

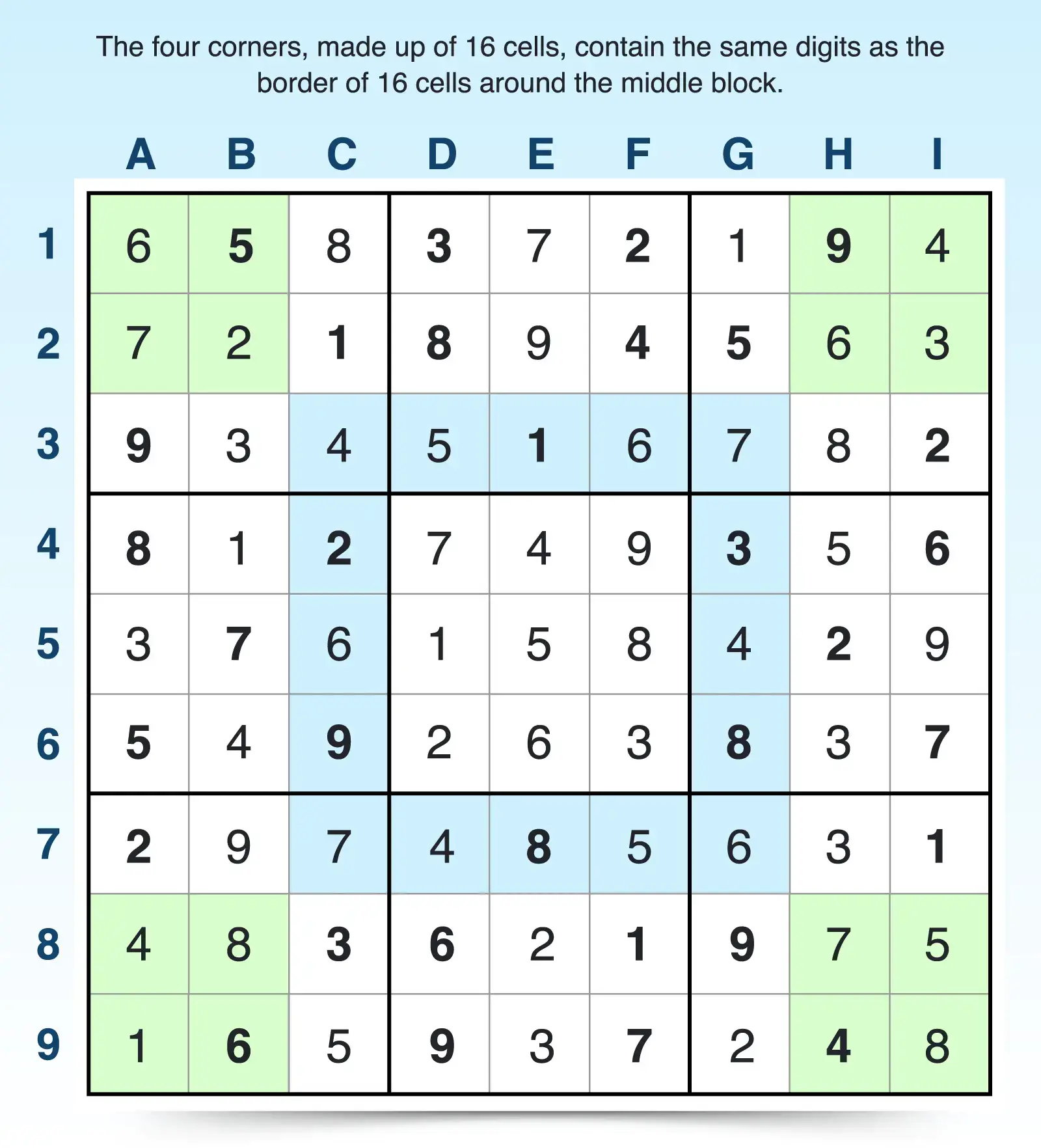
For example, this puzzle’s corners are filled out with the following answers:

• Top-right corner: 2, 5, 6, 7
• Top-left corner: 3, 4, 6, 9
• Bottom-right corner: 1, 4, 6, 8
• Bottom-left corner: 4, 5, 7, 8

With those cells filled in, you can see that the Phisotmefel ring must contain 1, 2, 3, 4, 4, 4, 5, 5, 6, 6, 6, 7, 7 8, 8, and 9. Looking at the 16 cells bordering the center 3x3 block, you see those same numbers in those same quantities filling the cells of the ring.

When it comes to solving puzzles, you know the digits and amount of times each digit appears must match as you fill in the corners and the ring. If any of those numbers are missing or the quantity is wrong (such as only two 4s appear when there should be three), you can compare the known answers in the corners to the ring and vice versa. This allows you to form a pool of numbers that are possible placements for those cells. After you notice further constraints, such as givens or other candidates that impact those cells, you can narrow down the possibilities even further.

Using the Phistomefel Ring to Find Answers

Using the Phistomefel ring technique is simply a balancing act. As you discover the number of appearances of one candidate in the four corners, you know it needs to appear that many times in the ring and vice versa. This knowledge can help you both eliminate and place candidates in cells in those areas (the ring and the corners).

As you solve a Sudoku puzzle, you can tally how many times a candidate appears in the

Phistomefel’s key areas. Creating a quick chart can help you keep track. For example, the puzzle below would use the following chart at its current stage of solving.

Corners	Sudoku Digit	Ring
1	1	0
1	2	2
2	3	0
0	4	2
0	5	2
0	6	1
2	7	1
0	8	1

The number of appearances for each digit will change as you fill in more answers, but this can help you narrow down possibilities as you analyze candidate numbers in the grid. For example, you know that 2 must appear at least twice in the corners because it currently appears two times in the ring (C6 and G3). But it currently appears just once in the outer corners (A1). Knowing it must appear at least one more time, you can look for possible placements.

You can use Sudoku scanning to determine:

• A 2 cannot be placed into column A or C, but column B currently has no 2s.
• Of the blocks connected with column B, the top-left block has a 2, the middle-left block has a 2, but the bottom-left doesn’t have a 2.
• The only open cells in that block are A7, B9, and C8, but because 2s appear in columns A and C already, 2 must be placed into B9, which is a corner area related to the Phisotmefel ring.

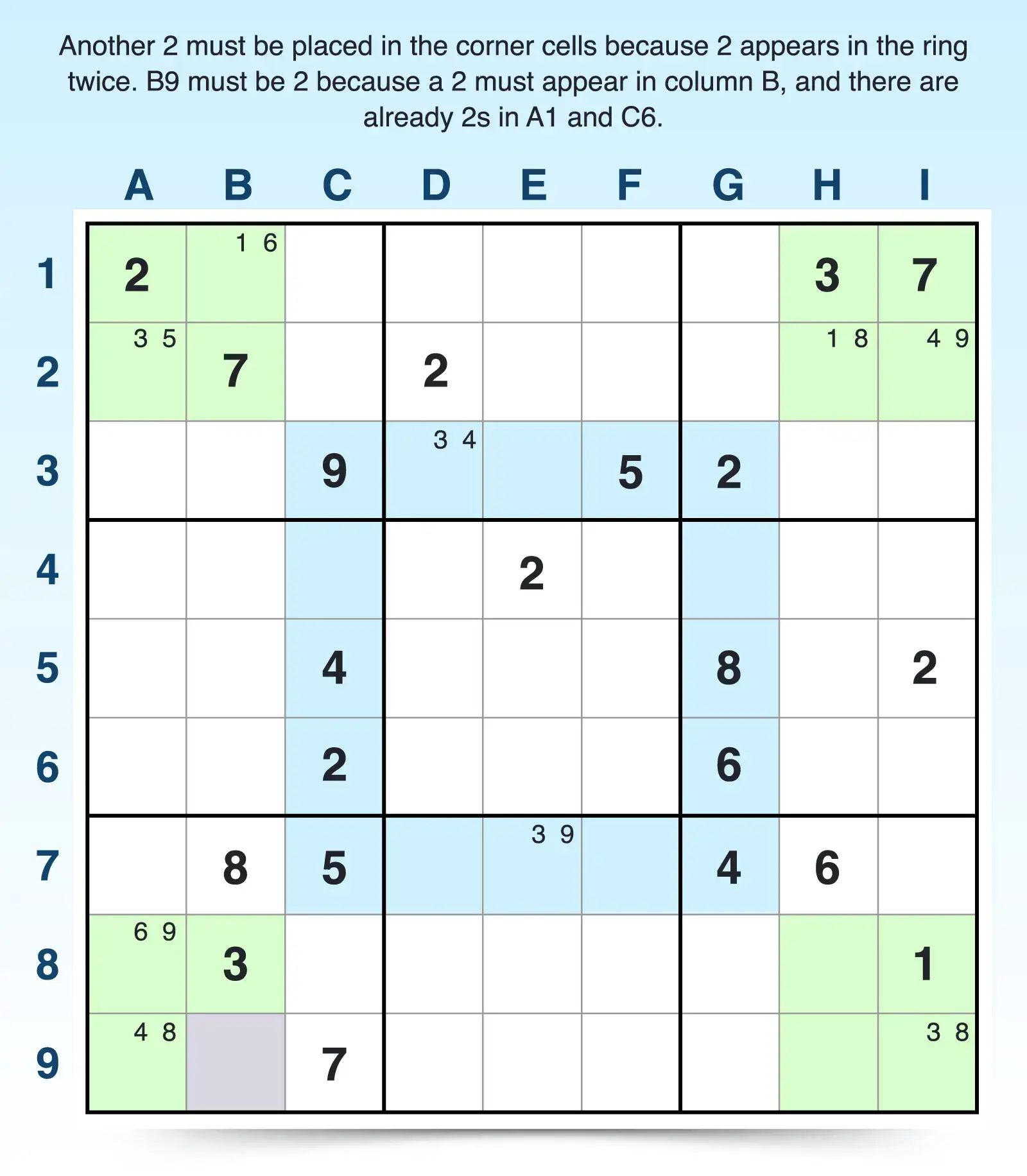Now the 2s are balanced, but both the ring and the corners still have open cells. Further scanning of the corner areas reveals:

• A 2 appears in columns G and I, but not in H.
• The top-right and middle-right blocks already have a 2.
• The bottom-right block has G8, G9, H8, H9, I7, and I9 as open cells.
• Only H8 and H9 are possible placements for 2.
• Because a 2 was placed in B9, a 2 must go into H8.

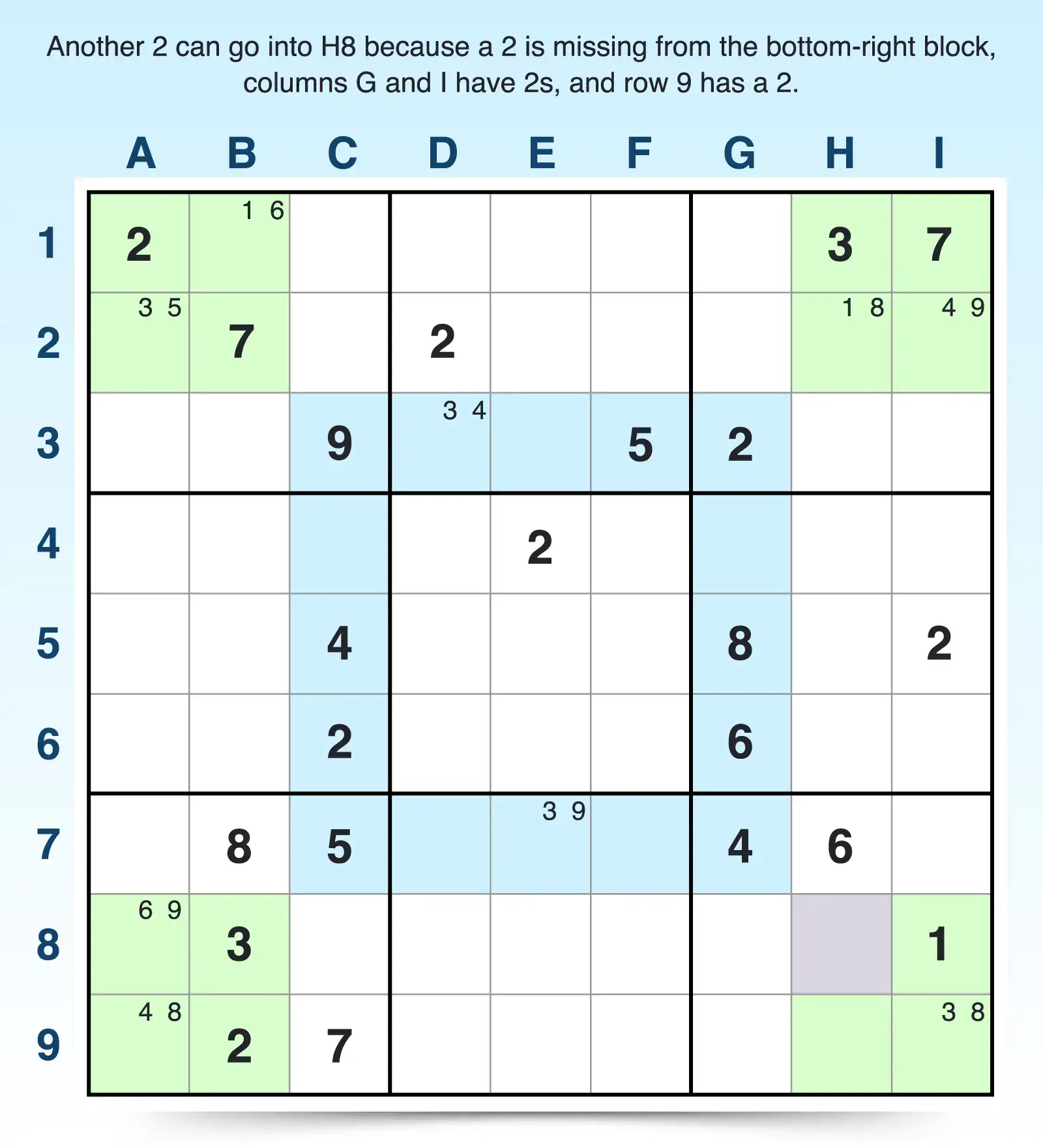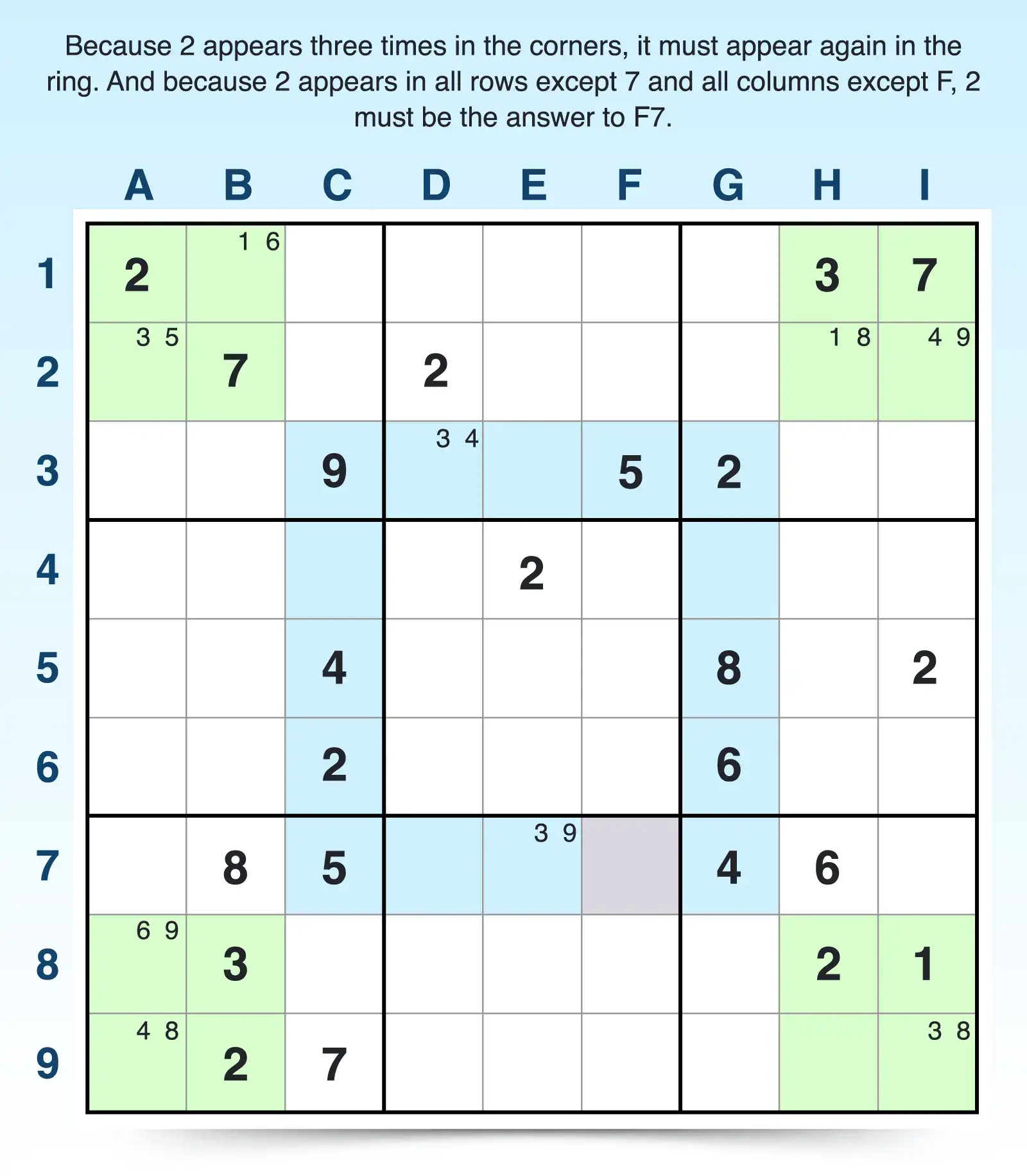
Now the 2s are out of balance again, but this time, 2s appear three times in the corner and just twice in the ring. Sudoku scanning can help you find the third placement of 2 in the ring:

• Only rows 3 through 7 are part of the ring. You can scan rows 3 through 7 and discover that a 2 already appears in rows 3, 4, 5, and 6, but no 2 is in row 7.
• Columns C through G are the only columns part of the ring. As you scan through those columns, you can see that all of them except F contain a 2.
• So 2 must be placed in F7.

The 2 is now balanced again. Because 2 appears in all columns and all rows, you can be sure that it won’t appear in the ring or corners anymore.

If you want to try out the Phistomefel ring technique in your next puzzle, play Sudoku online and include this in your next solving session!