The Snyder notation is a Sudoku technique where you place candidates only when a number can go in exactly two cells within a 3x3 block. It helps you spot naked and hidden pairs, eliminate extra candidates, and visualize patterns for advanced strategies.

This Sudoku strategy was developed by Thomas Snyder who won the World Sudoku Championship three times. The concept relies on the Sudoku rule that every unit (row, column, and block) must have numbers 1 through 9 placed in them only once. So marking candidates in boxes only when they have two possibilities helps narrow down placements and spot opportunities as the puzzle progresses.

Whether you’re a beginner looking to level up or an experienced solver aiming to cut solving time, the Snyder notation offers an efficient way to tackle puzzles when you play Sudoku online. This post details how to use the Snyder notation technique to solve Sudoku puzzles at all levels.

How to Use the Snyder Notation Technique

Snyder notation is most helpful when there are multiple givens per block or you can quickly narrow down two possible candidates. It may not be useful on sparse or expert-level puzzles until you place answers.

To utilize the Snyder notation technique, you simply mark candidates when the candidate is a possibility only twice in a 3x3 block. You can place the candidates using pencil marks in a paper-and-pencil puzzle or by using candidate mode online.

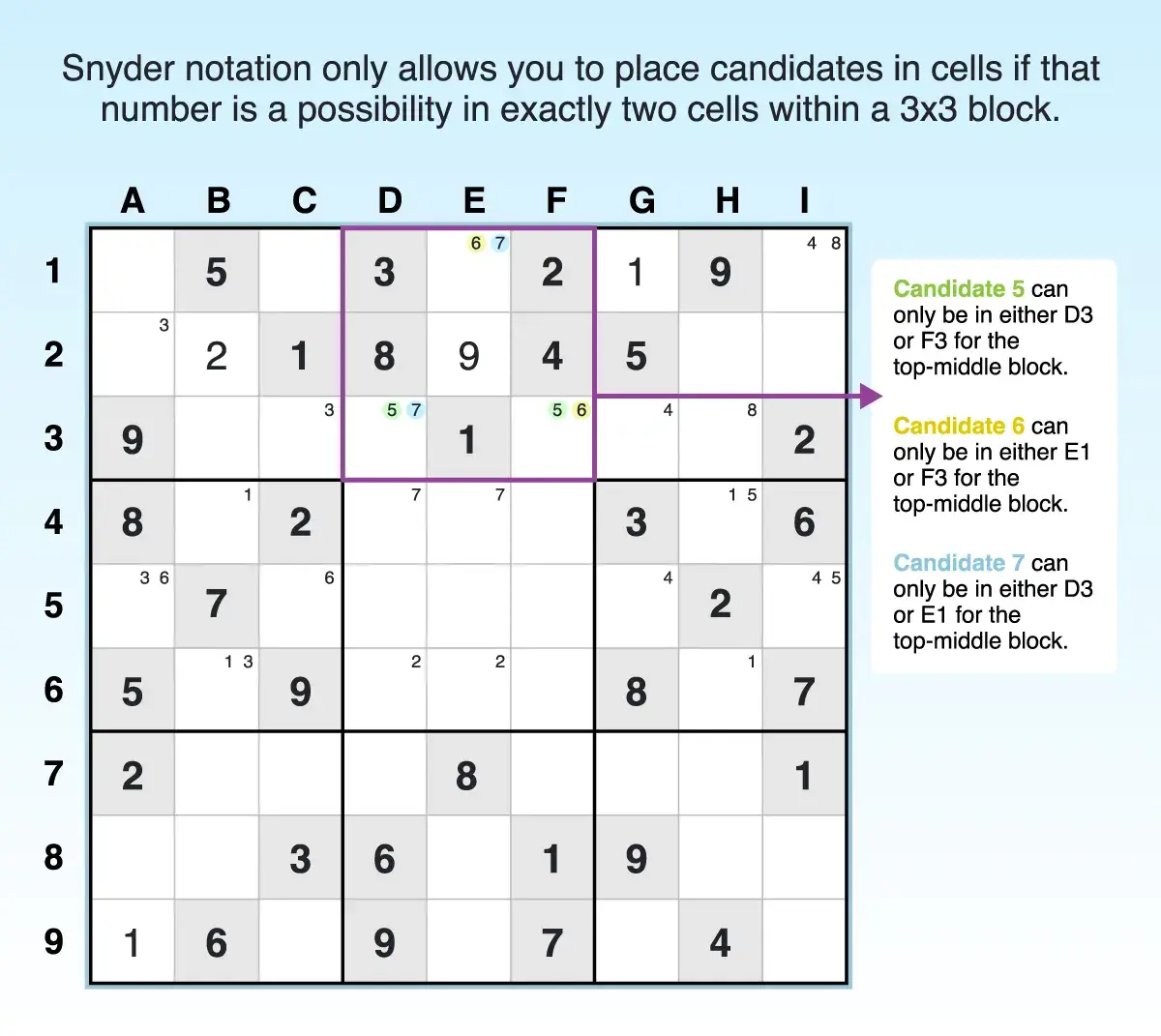
For example, in the top-middle block, candidate 5 could only be in either D3 or F3; candidate 6 could only be in either E1 or F3; and candidate 7 could only be in either D3 or E1.

To use the technique effectively, follow these tips:

• Find a block with a lot of givens or answers. The fewer empty cells left in a block, the better your chances for finding viable candidates for the technique. For example, the top-middle block has a lot of givens, so it makes for a good target in this technique.
• Use Sudoku scanning methodically to make placements, then rescan. Scan the block’s intersecting rows and columns to find answers and determine whether candidate numbers can be placed only twice. Doing this in numerical order (1 through 9) ensures you don’t miss anything. For example, scanning revealed that E2 was the only cell in which a 9 could be placed. Then rescanning revealed that candidates 5 and 7 could be added via Snyder notation.
• Avoid misidentification of naked singles. Because you only place a candidate when it has just two possibilities, it’s easy to scan the puzzle and think you’ve discovered naked singles, cells where all other candidates have been eliminated, leaving only one possible answer for that cell. When using Snyder notation, however, a cell may have other candidates, but they aren’t marked. For example, B4 and C5 look like only a 1 and 6, respectively, can be placed in those cells, but not all candidates are marked. Because candidate 4 is a possibility in all open cells in that block, B4 and C5 are not naked singles.
• Be patient. While you may end up with some cells with no candidates marked at all, you’ll still be able to make progress with your puzzle as you discover patterns that lead to eliminations and placements.

Snyder Notation Technique Examples

As you work through the grid, you’ll discover how easy it is to identify vital patterns that crack your puzzle wide open.

Creating a Cascade of Moves with the Snyder Notation Sudoku Technique

While finding hidden or pointing pairs can lead to several moves, simply using Snyder notation can do the same.

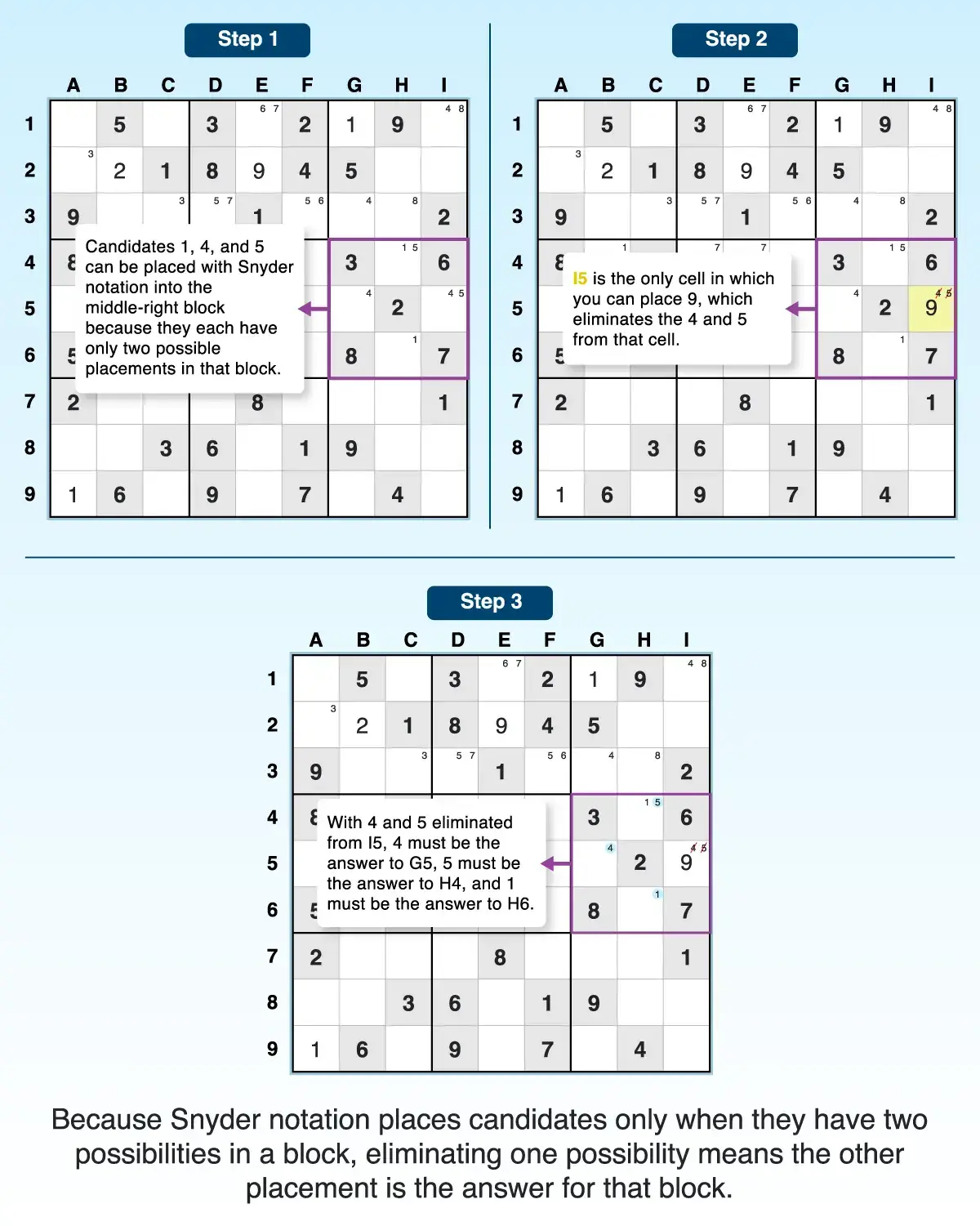
For example, the middle-right block had a lot of givens, and it was obvious that some candidates had just two possibilities in the block. However, 9 can only go into I5. After 9 gets placed in I5, it will create a cascade of moves:

• Because candidate 4 was eliminated from I5, G5 becomes the only spot in which 4 can be placed.
• Because candidate 5 was eliminated from I5, H4 becomes the only cell in which 5 can be placed.
• Because candidate 1 was eliminated from H4, H6 becomes the only cell in which 1 can be placed.

And those are just placements within the block. Because of the numerous placements, you can rescan other blocks to see if you can place or eliminate candidates with Snyder notation. For example, G3 will eliminate 4 as a candidate because it was placed in G5. That means I1 must be 4. You can keep working through the puzzle like this until you hit a roadblock or solve it completely!

Spotting Naked Singles with Snyder Notation

This technique can make naked singles shine like neon signs, but proceed with caution. Since you don’t note all possible candidates within a block when using Snyder notation, you may think you’ve spotted a naked single when another candidate could possibly be an answer to the cell.

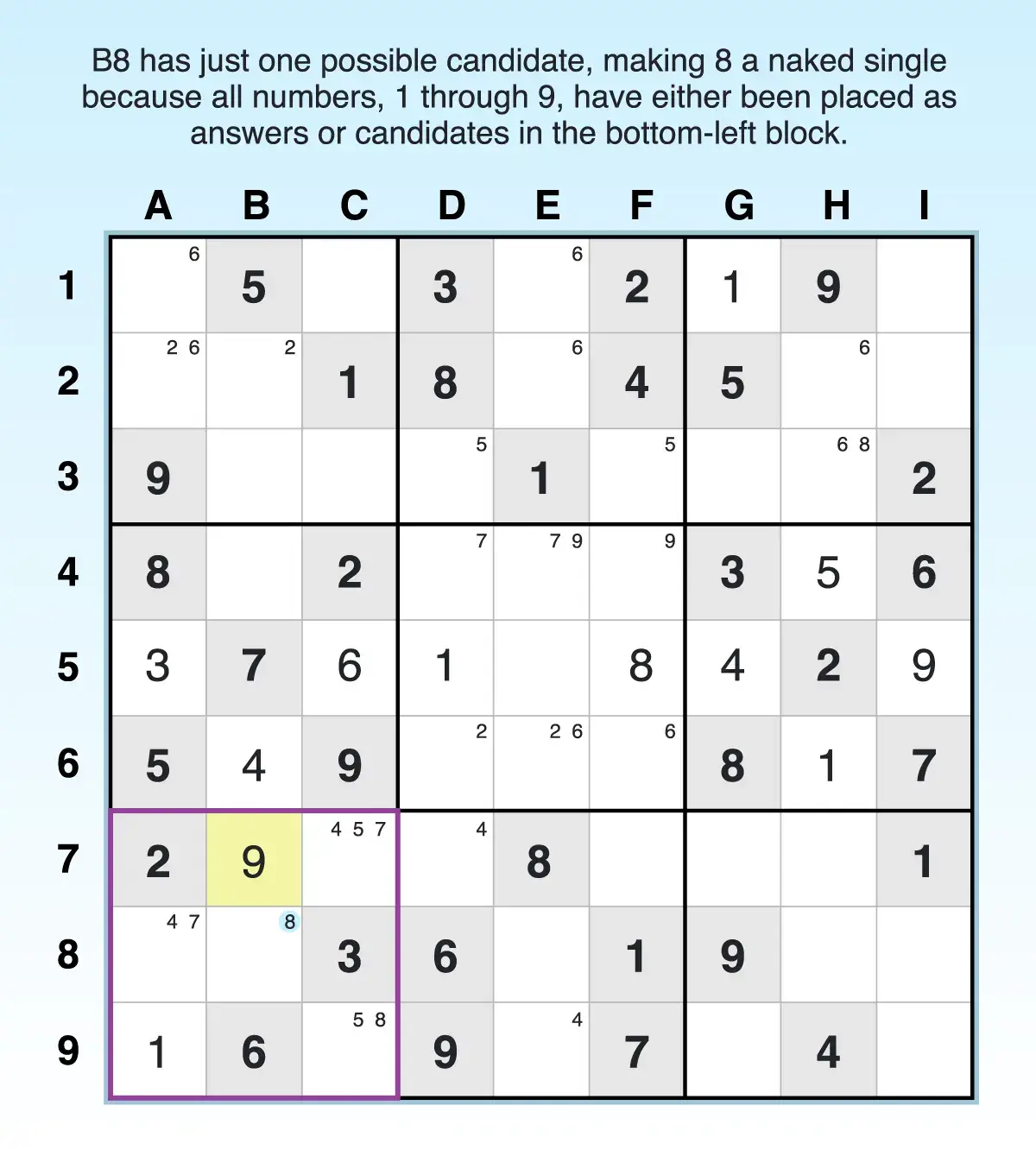
Before marking naked singles as the answer, be sure that all other candidates for that cell have been eliminated. For example, the bottom-left block has a single candidate (8) marked in B8. Because all candidates have been marked or placed as answers in that block, B8 has a naked single. Candidate 8 is the only number possible to be placed in that cell.

Because B8 must be 8, you can

• Eliminate it as a candidate in C9, making 5 the answer for that cell.
• Eliminate 5 as a candidate in C7, creating a naked pair (4, 7) in cells A8 and C7.

You can also find naked singles simply by finding an empty cell in a box. If you scan the puzzle and find a single empty cell in a box, such as B4, check to see if all other candidates have been accounted for. If only one candidate hasn’t been placed, it must be the answer for that cell.

Identify Pointing Pairs to Eliminate Candidates with Snyder Notation

Snyder notation helps you spot and use pointing pairs to eliminate candidates. A pointing pair occurs when a candidate appears in only two cells within a block, and both cells are in the same row or column. This lets you eliminate that candidate from the rest of the row or column outside the block.

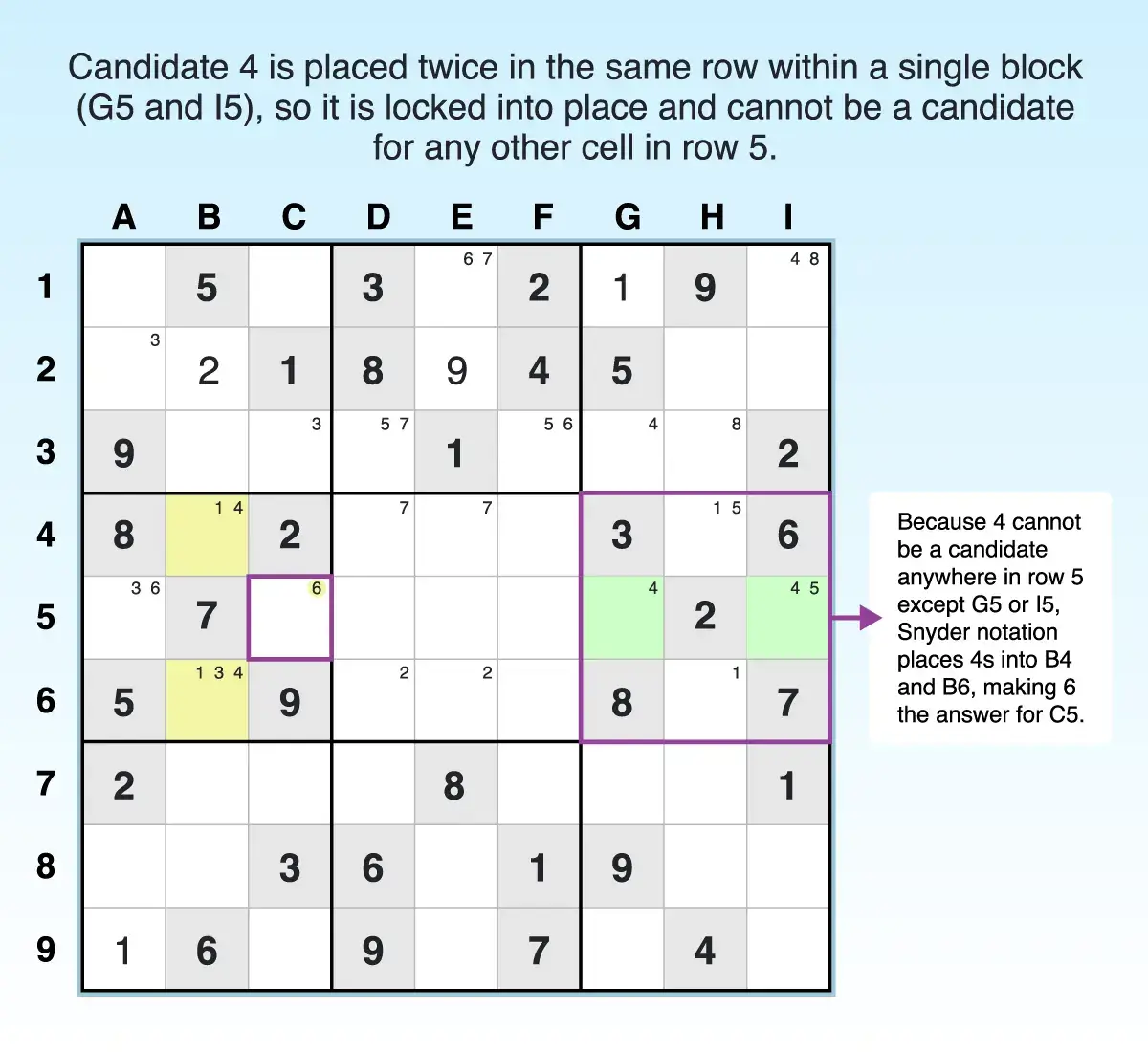
For example, row 5 has a pointing pair in G5 and I5. Because 4 is only a candidate in those two cells within the block, it can’t be placed elsewhere in the row. This leads to several subsequent moves:

• That means A5 and C5 can be eliminated as possibilities for candidate 4, allowing 4 to be placed as a candidate, using Snyder notation, into B4 and B6.
• Consequently, C5 ends up with a naked single (6).
Because C5 must be a 6, you narrow down the placement of 6 as a candidate in the first
• block and can use Snyder notation to add 6 as a candidate to A1 and A2.

Snyder notation cuts down the amount of candidates you have to manage, highlights patterns, and sets up cascading moves that simplify harder puzzles. By training your eye to spot pairs and use logical eliminations, this method reinforces core Sudoku strategies while boosting efficiency. Try Snyder notation on your next Sudoku puzzle and see how quickly it improves your solving!