XYZ-Wing: How to Find It & Eliminate Sudoku Candidates

Used as a candidate eliminator, the XYZ-wing strategy is similar to the XY-wing (also known as Y-wing), but the pivot has three possible candidates instead of two. This advanced technique helps you create precise eliminations in a Sudoku puzzle, often unlocking answers and causing chain reactions.

Whether you're building up from intermediate tactics or you're an advanced solver, the XYZ-wing fits naturally into your toolkit of Sudoku solving techniques. Use our simplified explanation, clear steps to spot it, and examples so that you can start using this technique when playing Sudoku online.

Simplifying the XYZ-Wing Technique

To find an XYZ-wing, look for three linked cells—one pivot and two pincers—that revolve around a common candidate number (call it z).

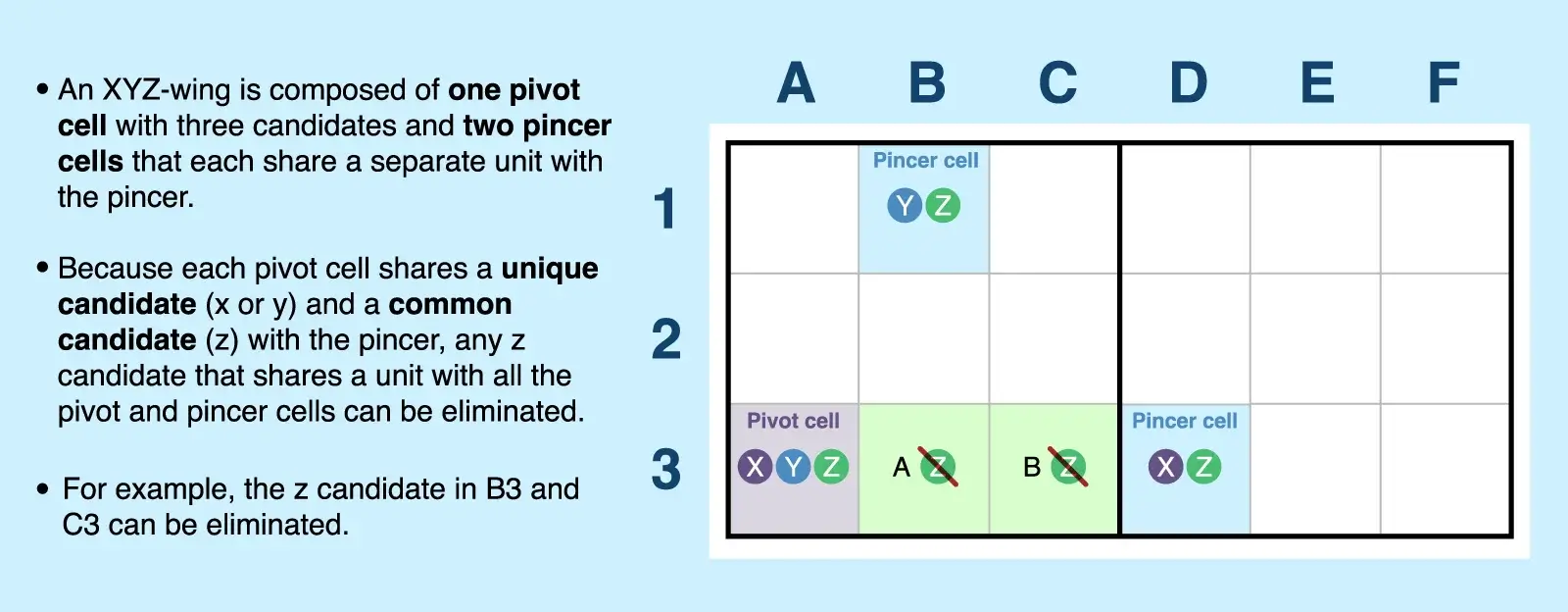
• Pivot cell: A three-candidate cell with candidates x, y, and z. It shares a unique unit with each pincer cell, which means the pivot cell "sees" both pincers. For example, A3 is the pivot with x, y, and z as its candidates.
• Pincer 1: A bi-value cell (a cell with only two candidates) with candidates x and z. This pincer shares only one unit (row, column, block) with the pivot. For example, D3, shares a row with the pivot cell and contains candidates x and z.
• Pincer 2: A bi-value cell with candidates y and z. This pincer shares a different unit (row, column, block) with the pivot. This pincer doesn't have to share a unit with the other pincer. For example, B1, shares a block with the pivot cell and contains candidates y and z.

Because both pincers see the pivot cell, then z has to be the answer in one of the three cells. So any cells that share a unit (or see) all three of the cells can eliminate the z candidate. In this case, you can eliminate z in B3 and C3.

How to Find a Sudoku XYZ-Wing

This advanced strategy is simple to apply when you know what you're looking for. Use these steps to locate the cells that make up an XYZ-wing:

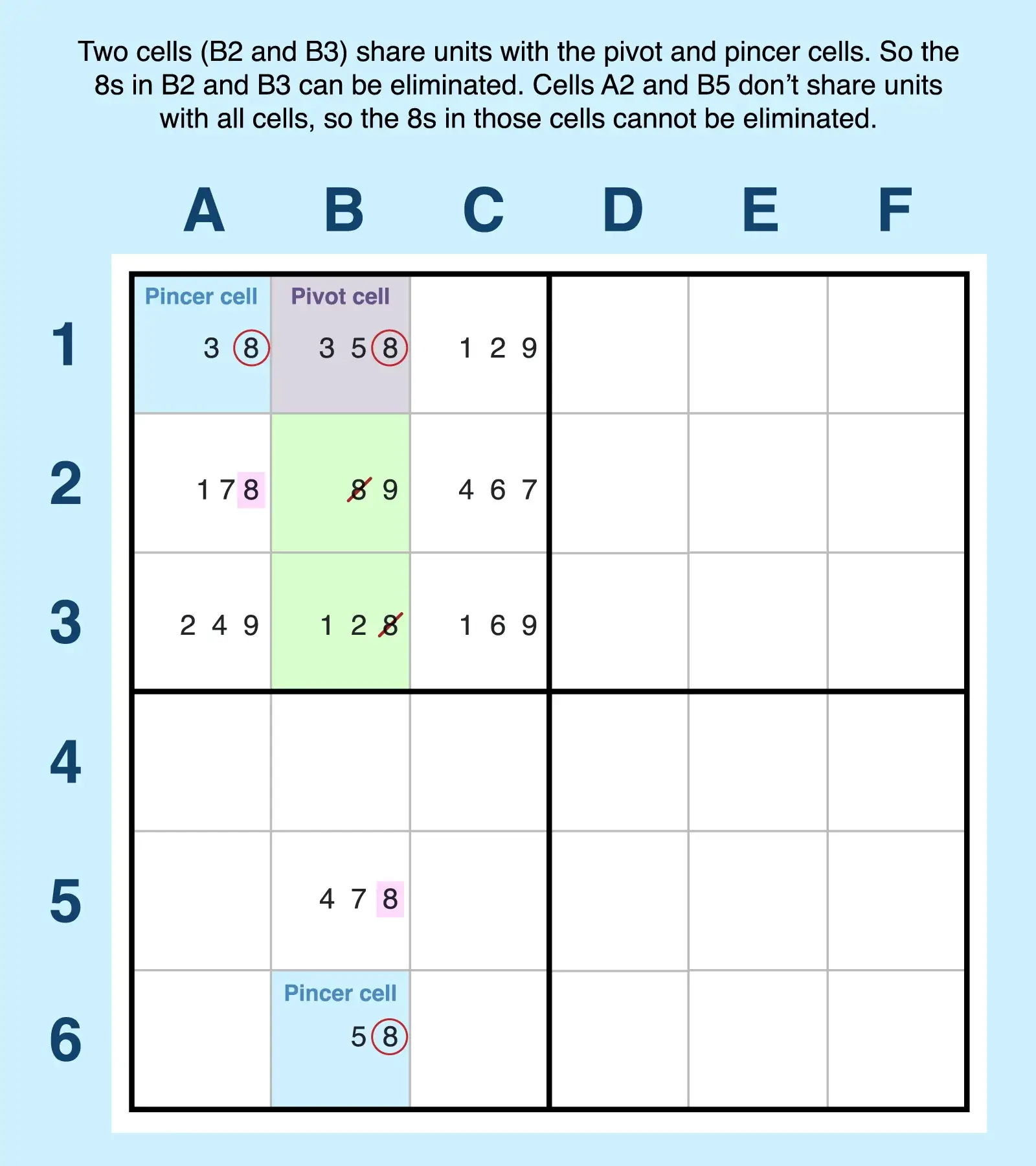
1. Find the pivot cell. Look for a cell that fits the following criteria:
   • It has three candidates (xyz). B1 has candidates 3, 5, and 8.
   • It can see two bi-value pincer cells with subsets of its candidates. B1 can see bi-value cells A1 and B6, which contain subsets of B1's candidates.
2. Confirm the pincers. For the pincers to be valid, they must follow this criteria:
   • Each must contain subset candidates xz and yz. For example, A1 has 3 (x) and 8 (z), B6 has 5 (y) and 8 (z); 8 is the common candidate (z).
   • Both must share different units with the pivot cell. For example, A1 shares the row and block, while B6 shares the column.
3. Find the target cells for elimination. Any cells that see all three cells of the pattern can eliminate candidate z. For example, B2 and B3 share a block with the pivot and one pincer (A1) and a column with B6. So 8 (candidate z) can be eliminated from those cells (B2 and B3). Cells A2 and B5 don't share units with all three wing cells, so the 8s in those cells cannot be eliminated.

XYZ-Wing Examples

Depending on how far apart the cells are, you typically get two cells to target for elimination. If they're spread too far apart, the cells won't see any of the same cells, leaving you with no cells to target for elimination. Proximity primarily impacts the ease with which you can spot the XYZ-wing.

XYZ-Wing Cells in Close Proximity

XYZ-wings are easier to confirm when the pivot shares a block with one pincer and a row or column with the other.

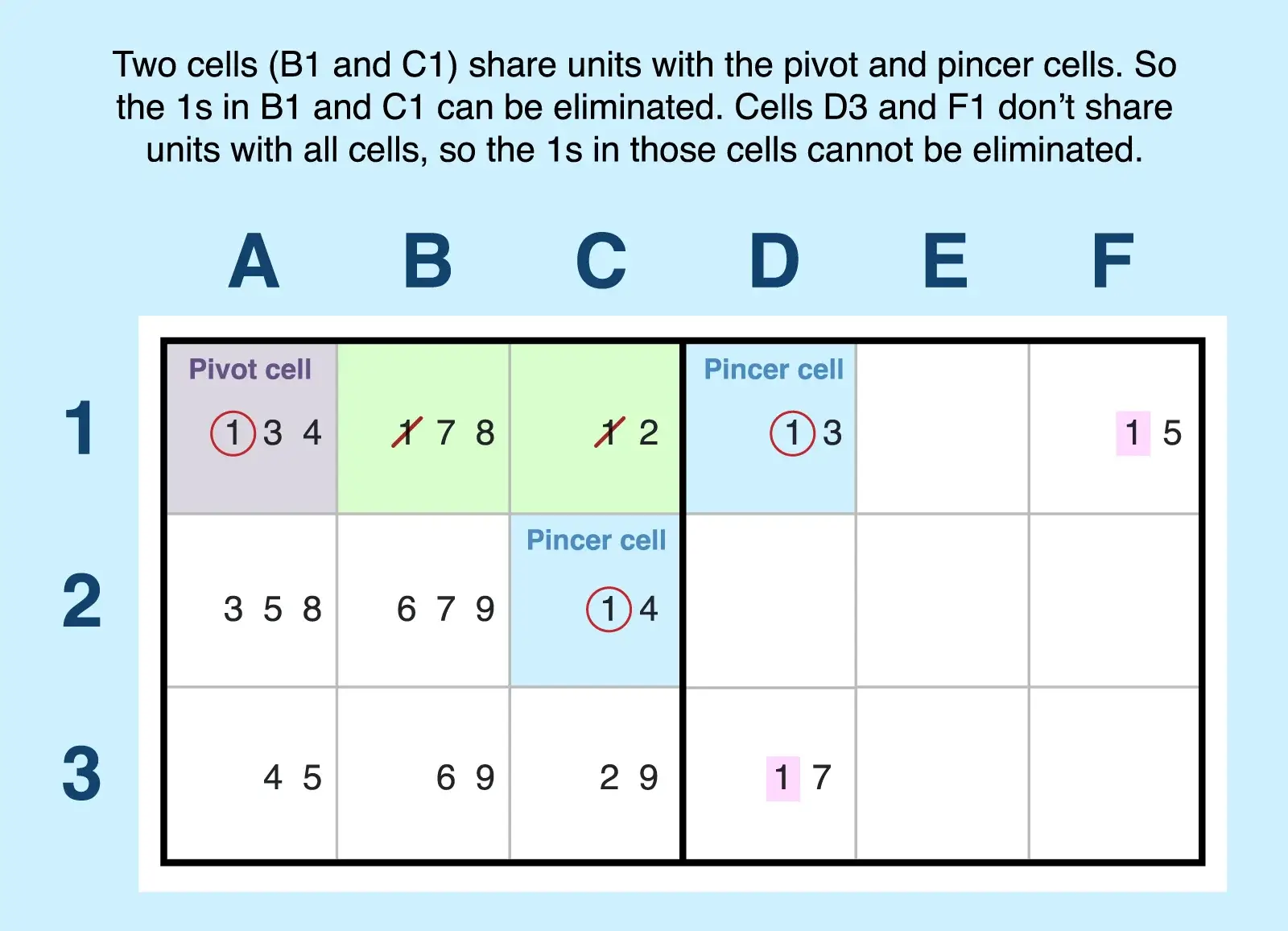
1. Find the pivot. A1 has candidates 1, 3, and 4 and can see bi-value cells D1 and C2. Both of these cells have subsets of the candidates in A1.
2. Confirm the pincers. D1 contains 1 (z) and 3 (x) and shares a row with A1. C2 contains 1 (z) and 4 (y) and shares a block with A1. So both are valid pincer cells.
3. Find the target cells for elimination. You can eliminate z (1) from any cells that see all three cells of the pattern. For example, B1 and C1 share a block with the pivot (A1) and one pincer (C2) and a row with the other pincer (D1). So 1 can be eliminated from those cells (B1 and C1). Because cells D3 and F1 don't share units with all three cells, the 1s can't be eliminated in those two cells.

This setup is about as close as an XYZ-wing can be. If all three cells of the wing are in the same 3x3 block, conceivably, all the other cells in the block would be targets to eliminate candidate z. But in this case, XYZ-wing is the weaker strategy. If three cells that share the same three or subsets of the same three candidates, you have a naked triple, which offers even more elimination possibilities.

XYZ-Wing Cells Spread Farther Apart

When the XYZ-wing is spread farther apart, it can be more difficult to spot the actual wing. So be sure to scan units for a cell containing three candidates, checking them for bi-value cells with shared candidates.

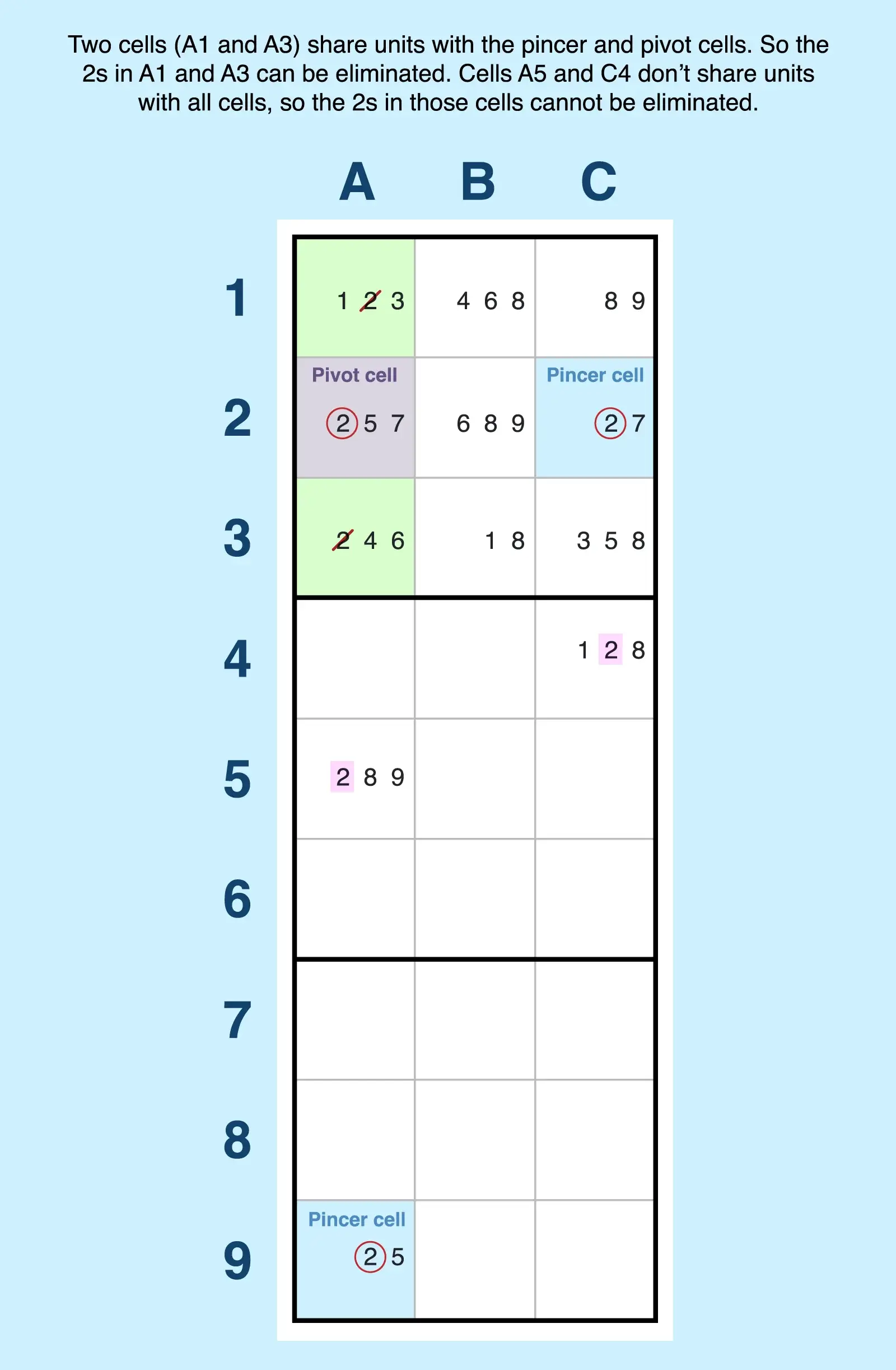
1. Find the pivot. A2 has candidates 2, 5, and 7 and can see bi-value cells C2 and A9. Both of these cells have subsets of the candidates in D1.
2. Confirm the pincers. A9 contains 2 (z) and 5 (x) and shares a column with A2. C2 contains 2 (z) and 7 (y) and shares a block and row with A2. Both are valid pincer cells.
3. Find the target cells for elimination. You can eliminate z (2) from any cells that see all three cells of the pattern. For example, A1 and A3 share a block with the pivot (A2) and one pincer (C2) and a column with the other pincer (A9). So 2 can be eliminated from those cells (A1 and A3). Because A5 and C4 don't share units with all three wing cells, you can't delete the 2s from those cells.

Practice Finding an XYZ Wing

Before you add this technique to your existing Sudoku strategies, you can practice on the puzzle below. Look for a pivot cell and two bi-value pincers to determine what cells to target for candidate elimination. If you need help, just click the hint button and use the arrows to click through the messages.

If you're finding close variations of an XYZ-wing but not the exact pattern, don't be discouraged. You could be finding other useful patterns like W-wings or X-wings. These techniques can also help you find a common number among cells that can be eliminated, which could be the one number you need to unlock an expert or evil-level puzzle when you're playing Sudoku online.