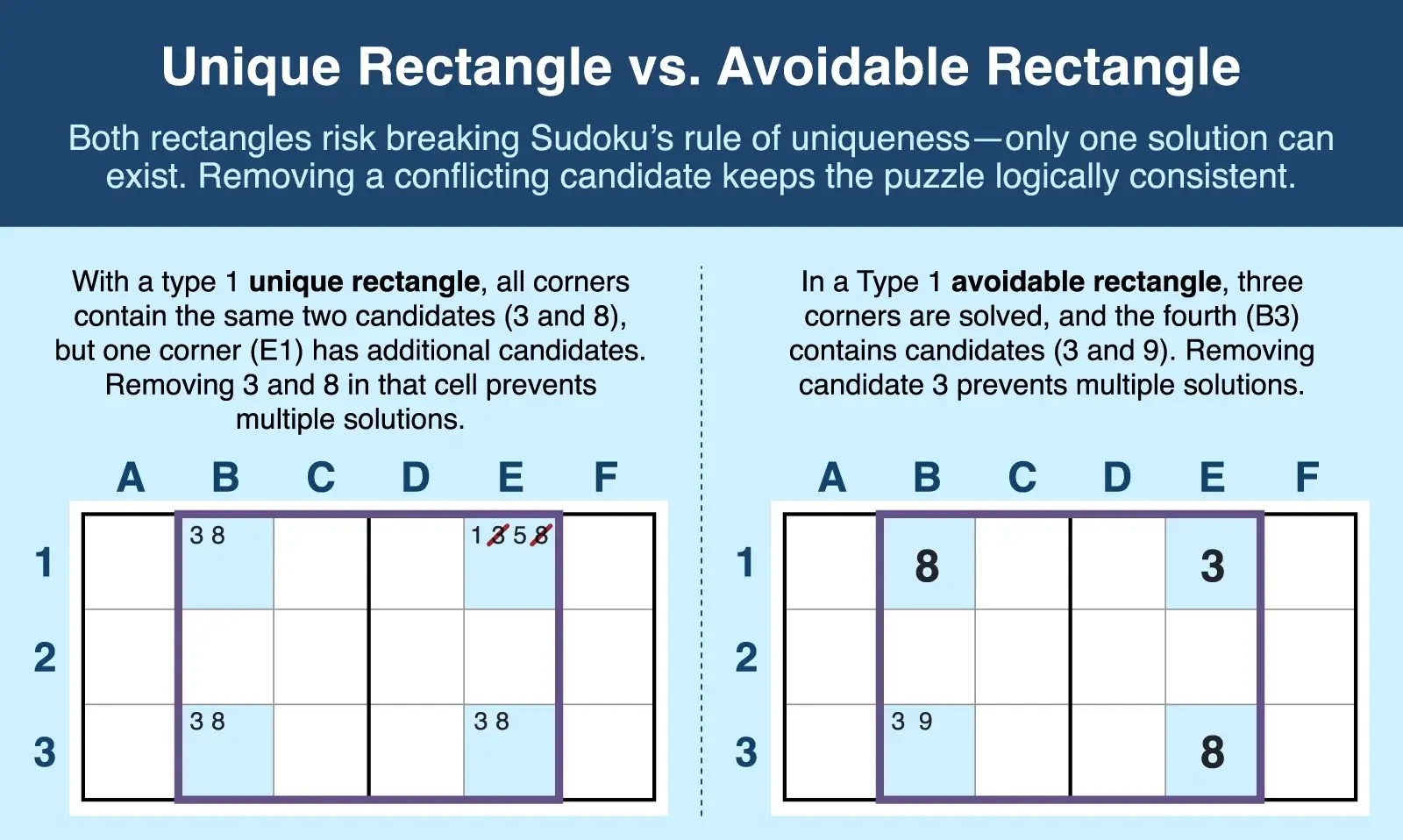
An avoidable rectangle is a Sudoku solving technique used to prevent a deadly pattern—when the placement of candidates leads to more than one puzzle solution. It occurs when two or three corner cells of a rectangle contain answers and at least one corner is still unsolved. By eliminating the candidate that might create multiple solutions, you preserve the puzzle’s uniqueness and avoid creating interchangeable answers across the rectangle.

Although an avoidable rectangle looks similar to a unique rectangle, it forms and solves differently:

• Unique rectangles are derived from four unsolved cells with candidates and rely on the uniqueness test—the assumption that a puzzle must have only one solution. You use that assumption to eliminate or confirm extra candidates.
• Avoidable rectangles occur when two or three cells have been answered, locking in part of the rectangle. In this case, the solved cells prove that keeping a particular candidate in an unsolved cell would create two interchangeable solutions, which directly violates Sudoku logic. This allows you to eliminate or confirm candidates in the unsolved cells.

Because avoidable rectangles often appear after progress has already been made in a puzzle, they offer a practical advanced technique you can utilize with harder Sudoku puzzles.

How to Find Avoidable Rectangles

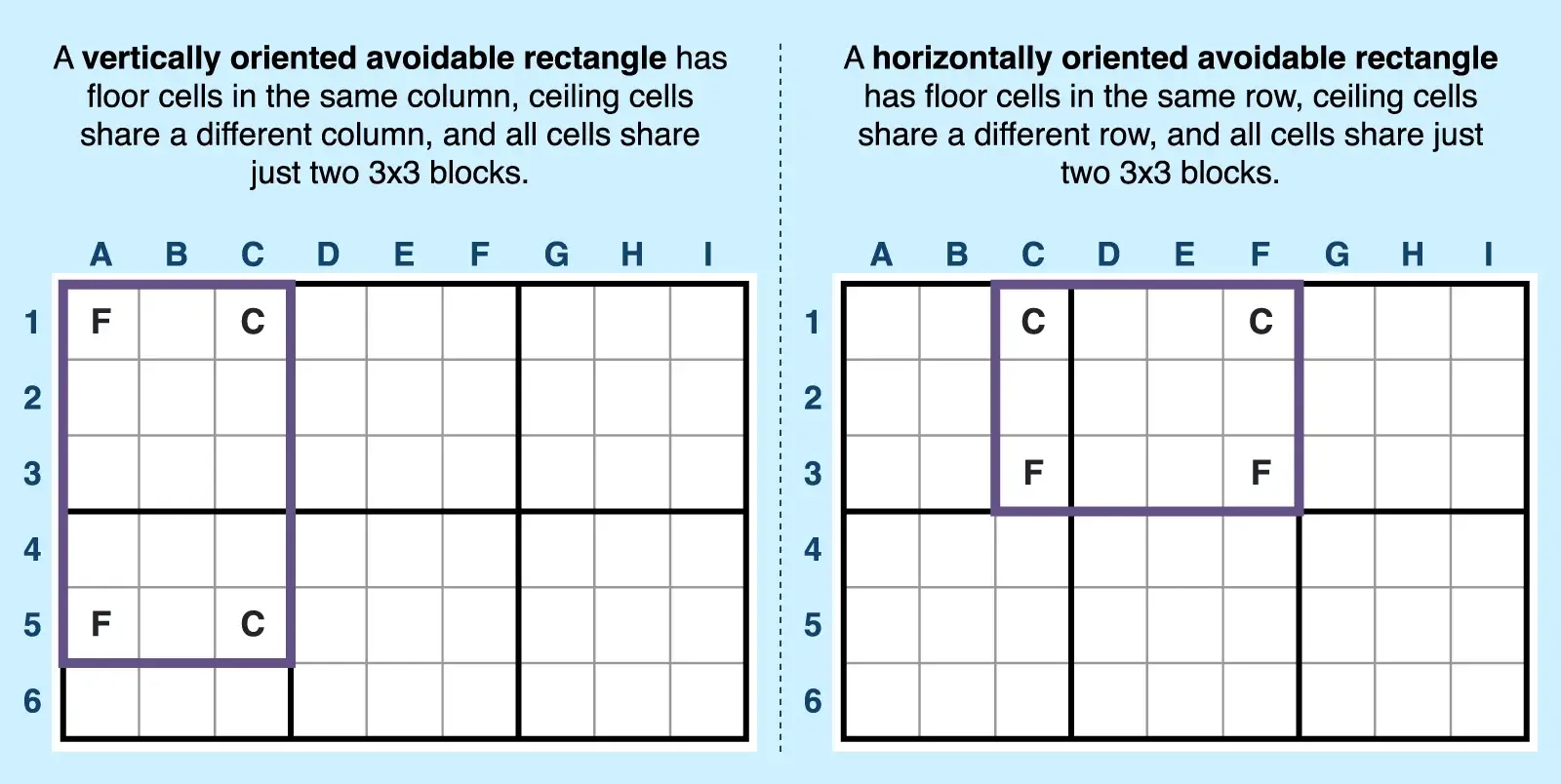
Avoidable rectangles share two rows and two columns to create the rectangle shape, but they also share two 3x3 blocks. You can find a Type 1 or Type 2 avoidable rectangle by following these steps.

1. Find two floor cells. Ensure that two cells share a row or column and have answers (not givens). These solved cells anchor the rectangle. In the examples below, floor cells are marked with an F.
2. Find the matching ceiling cells and confirm all four cells are within two blocks. Both ceiling cells will create two more corners of the rectangle, and all four candidates cover only two blocks. One or both cells will contain candidates, but neither ceiling cell will contain givens. In the examples below, the ceiling cells are marked with C.
3. Check the relationship between the answer and the candidate cells.The answer cells involve only two digits. Candidate cells must include one or more of these digits, and in Type 2, they must also share an additional common candidate. This setup allows eliminations because, if left unresolved, the rectangle could produce multiple solutions, breaking Sudoku’s uniqueness rule.

Avoidable rectangles can be oriented vertically, where floor cells share a column and ceiling cells share a separate column, or horizontally where floor cells share a row and ceiling cells share a separate row.

Avoidable Rectangle Examples

The type of avoidable rectangle you find in a puzzle determines what candidates can be eliminated.

Avoidable Rectangle Type 1

Type 1 avoidable rectangles contain answers in three corners, and the answers consist of just two digits. The last corner contains one candidate that matches a number in the solved cells and at least one extra candidate. The candidate shared with the solved cells acts as an interchangeable "wild card" that could lead to a puzzle having more than one solution. By cutting that extra option, you keep the puzzle consistent and logically solvable for a single solution.

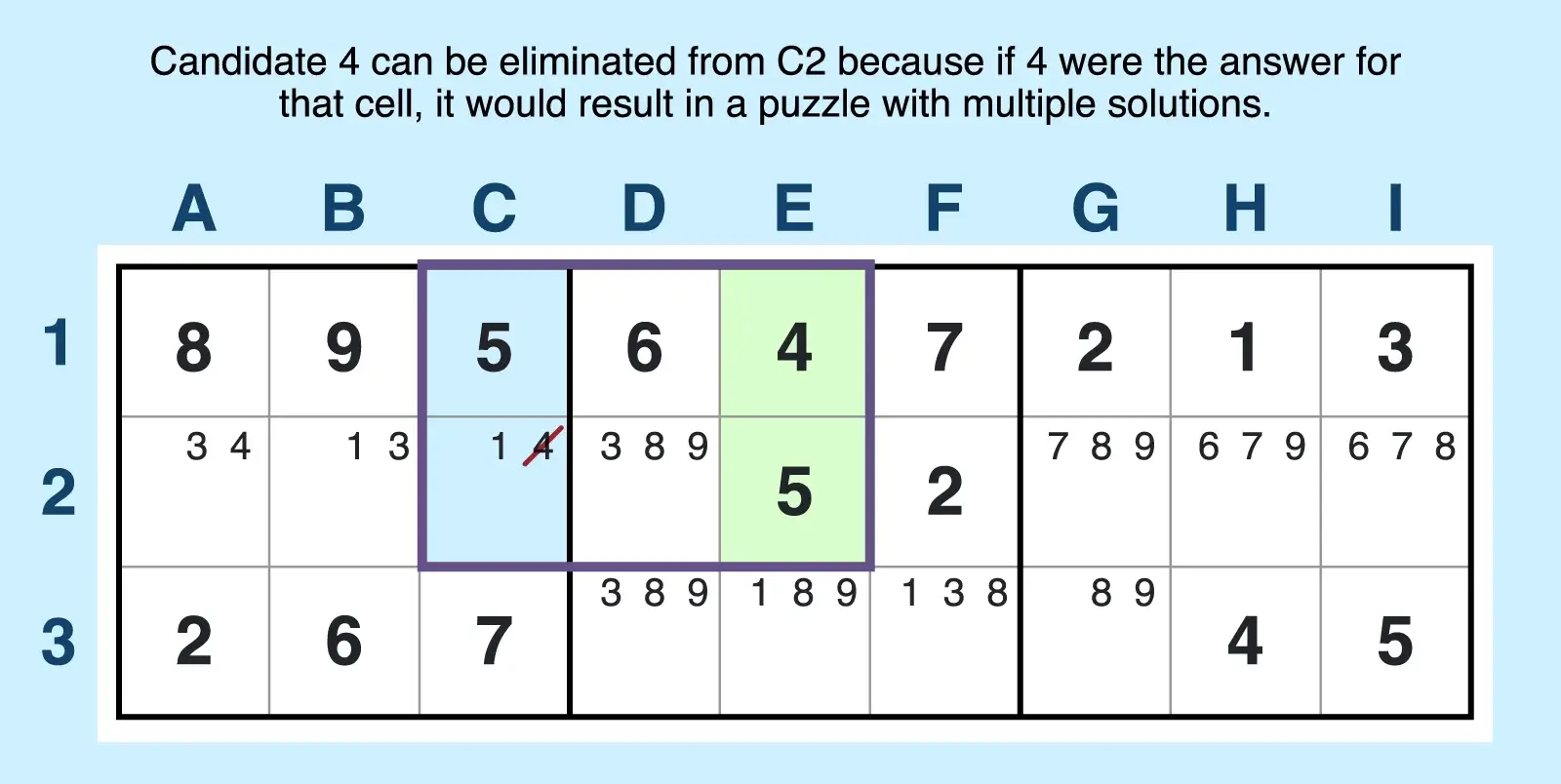
Find a type 1 avoidable rectangle by following these steps:

1. Find two floor cells that contain answers. For example, cells E1 and E2 appear in the same column and contain answers, not givens, to anchor the rectangle.
2. Find two ceiling cells—one that is answered and one that has candidates. For example, cells C1 and C2 form the other corners of the rectangle with E1 and E2, and all four cells are within just two blocks. Cell C1 is answered, but cell C2 contains candidates.
3. Verify that the answered cells include only two different digits. The answers in cells C1, E1, and E2 consist of just two digits (4, 5).
4. Confirm that the fourth cell contains at least one of the digits from the answered corners as a candidate plus one extra. The fourth corner (C2) contains two candidates. One candidate (4) is one of the answers from the three solved corners, but 1 is an extra candidate.

Candidate 4 can be eliminated from C2 because if 4 were the answer, the puzzle would have two solutions with 4 and 5 acting as an interchangeable pair within the four cells of the rectangle. So 1 must be the answer for C2 to maintain one unique solution for the puzzle. Unlike other techniques, such as X-wing, you’re eliminating a candidate from a cell within the pattern, not candidates in other cells outside of it.

Avoidable Rectangle Type 2

A type 2 avoidable rectangle has just two solved cells. The other two cells must contain candidates that match the solved cells as well as a shared candidate. In this type, the extra candidate must be the answer in one of those two unsolved cells, which allows you to eliminate it elsewhere in any unit those two cells share.

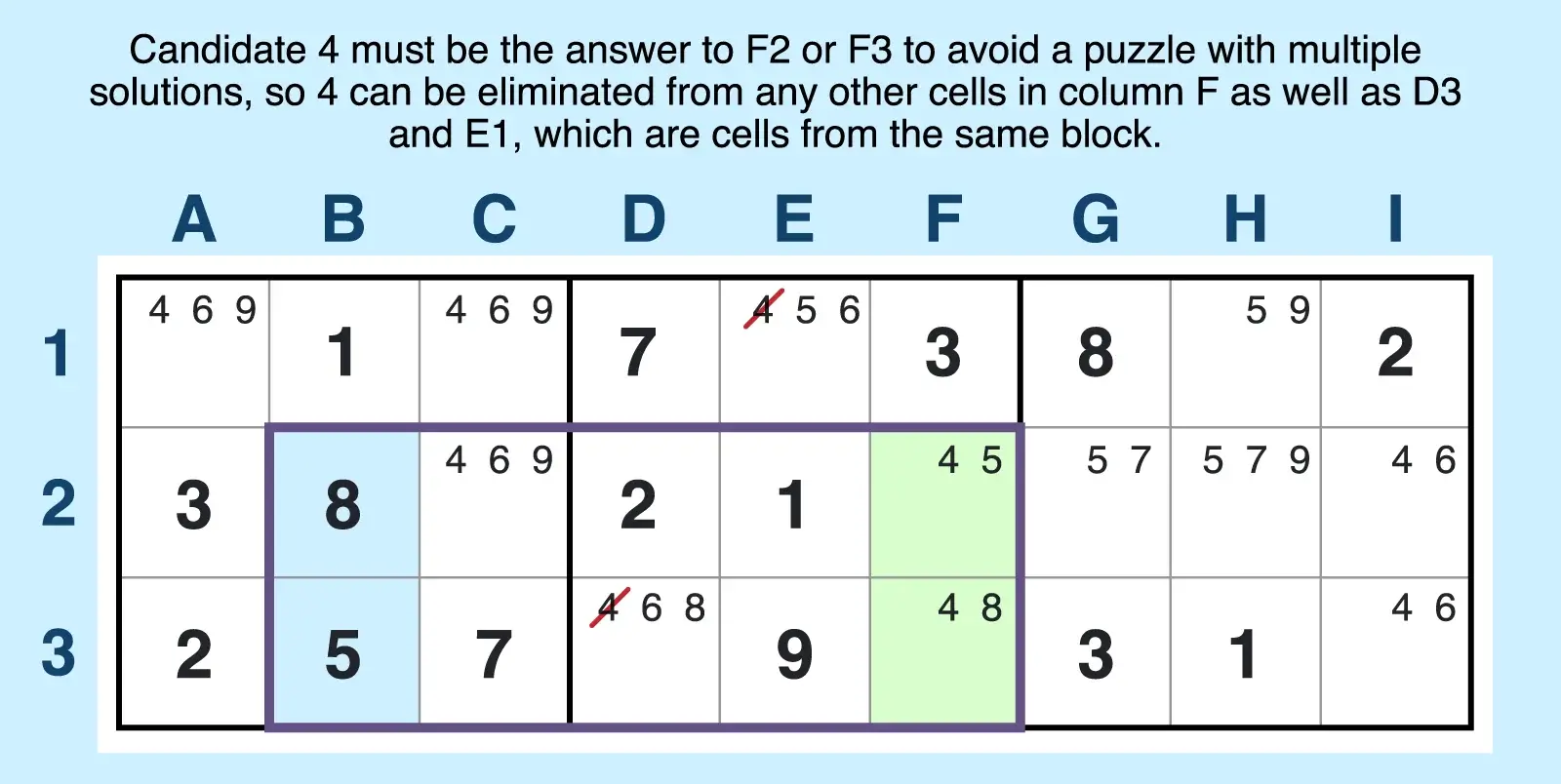
Find a type 2 avoidable rectangle following these steps:

1. Find two floor cells that contain answers. For example, B2 and B3 act as the floor cells. They contain answers (8, 5).
2. Find two ceiling cells, both of which contain candidates. Cells F2 and F3 both contain candidates, and all four cells create four corners of a rectangle and fall within two blocks.
3. Verify that each cell has one candidate that matches one of the answered cells as well as a shared candidate. Cells F2 and F3 each have a candidate that matches the solved cells (8 and 5) as well as a shared candidate (4).

Candidate 4 must be the answer to either F2 or F3 to avoid having a puzzle with multiple solutions. So 4 can be eliminated as a candidate within any unit both of those cells share. That means 4 can be eliminated from other cells in column F as well as from cells D3 and E1 because they share the same 3x3 block.

As long as you follow the specific criteria for each avoidable rectangle type, Sudoku solvers at all levels can use this technique when solving expert or evil-level puzzles because they have fewer givens.