The empty rectangle technique is a Sudoku elimination you apply when a candidate in a 3x3 block appears in only one row and one column within that block. The remaining four cells do not contain the candidate, forming an "empty rectangle."

If the same row or column outside the block contains a strong link (conjugate pair) for that digit, the pattern creates a contradiction. That contradiction lets you remove the candidate in the cell that sees these two elements: the restricted row or column of the block and the end of the strong link. It's a powerful way to make progress in hard Sudoku puzzles without needing a long chain or loop.

How to Find an Empty Rectangle in Sudoku

The empty rectangle is a pattern using all nine cells within one block of a Sudoku puzzle. However, the "empty" part of the pattern helps only with finding a useful block as well as the logic behind technique. It doesn't help you make the elimination. So understanding how the pattern is formed and how it works can help you find and use the pattern to skillfully eliminate candidates in Sudoku puzzles.

The Basic Empty Rectangle Pattern

An empty rectangle pattern is always restricted to one 3x3 block and is made up of two basic parts:

• A five-cell shape with the target number falling in exactly one row and one column, forming an L, T, or plus sign. These five cells are the only ones in the block that may contain the candidate, but not all of them need to actually hold it. Even if only one cell contains the candidate, as long as it lies in the intersecting row and column, the pattern is still valid. For example, cells A1, B1, C1, C2, and C3 create an L shape, and C1 contains the target candidate number (3).
• The four empty rectangle cells: The four other cells in the block are not empty cells. They just cannot contain the target number, and together, those four cells create an empty rectangle because they are empty of the target number. For example, A2, A3, B2, and B3 create the empty rectangle because they don't contain the target candidate number (3). The cells don't have to be adjacent to each other to be valid.

Spotting and Using the Empty Rectangle

To make an elimination with the empty rectangle solving technique, you need both an empty rectangle pattern and a conjugate pair (when a candidate has only two possible placements in a row, column, or block) that does two things:

• Shares the target candidate number with the empty rectangle
• Forms an empty rectangle intersection, meaning one cell of the conjugate pair aligns with the row or column of the empty rectangle that contains the target candidate

Find and use an empty rectangle pattern by following these steps:

1. Find an empty rectangle pattern in a 3x3 block. It should have:
   • A candidate is restricted to exactly one row and one column. For example, cells A5, B4, B5, B6, and C5 are in exactly one row and one column, and they are the only cells in the block that contain candidate 6, forming a plus-sign shape.
   • Four cells outside of the row and column do not contain the candidate number. Cells A4, A6, C4, and C6 don't have a 6. Because those four cells are empty of 6s, they create the literal empty rectangle.
2. Locate a conjugate pair of the target number that meets the following criteria.
   • The pair appears in two different blocks. For example, the only 6s in column F are in two cells (F3 and F5), making a conjugate pair. Both cells also appear in two separate blocks (top middle and absolute middle blocks).
   • At least one conjugate pair cell shares a row or column with a cell in the pattern that contains the target candidate. For example, the 6 in F5 shares a row (row 5) with the cells containing the target candidate in the plus-sign pattern, but F3 doesn't.
3. Use the conjugate pair to make eliminations outside of the empty rectangle block. To make eliminations, do the following:
   • Consider the candidate in the same row as the pattern to be x. For example, x would be the 6 in F5 because it shares the row with the cells containing a 6 in the plus sign. The same can be true if the candidate shares a column with the plus-sign pattern.
   • Consider the candidate that doesn't share the row with the pattern as y. For example, because F3 doesn't share a row or column with cells in the pattern containing 6, the 6 in this cell would be y.
   • Eliminate any candidate number in the column of the empty rectangle pattern that can see y. For example, B3 has a 6, and that cell shares the column of the plus-sign shape as well as the row of y. So the 6 in that cell can be eliminated, but the 6 in A3 cannot. It shares a row with y, too, but it doesn't fall in the same column (B) as the plus-sign shape.

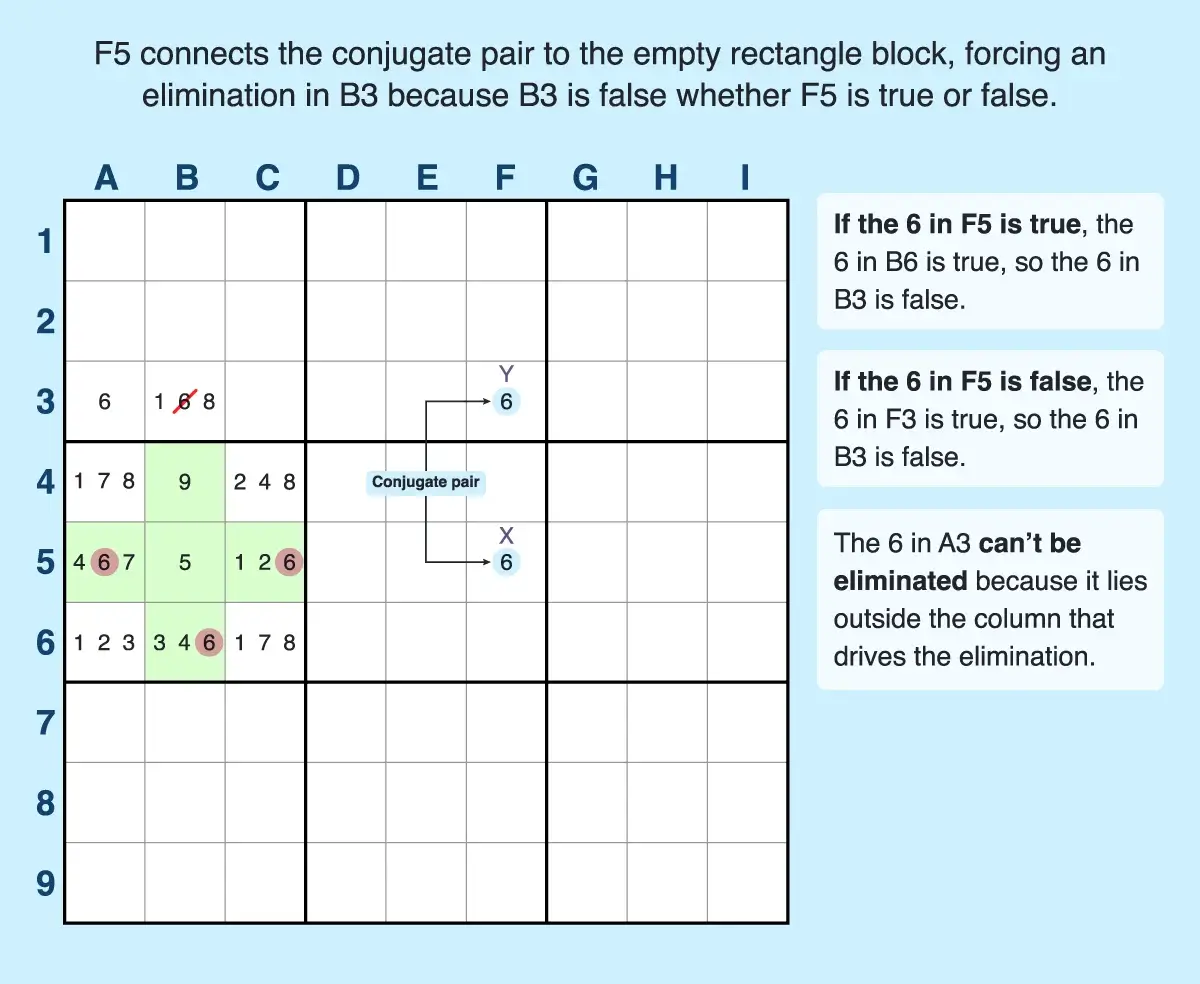
Empty Rectangle Logic

• If the 6 in F5 is true, then the 6s in row 5 of the plus-sign shape would be eliminated, and the 6 in cell B6 would have to be the answer for that block, thus eliminating the 6 in B3.
• If the 6 in F5 were false, then the 6 in F3 would have to be true, which would mean the 6 in B3 would have to be eliminated.
• Either way, the 6 in B3 has to be eliminated. The same can't be said for the 6 in A3 so it cannot be eliminated with this pattern.

Solving tip: If x shares a row, the elimination is made in the column of the shape for any cell that shares a unit with the y candidate's cell. If x shares a column, then the elimination is in the row.

Empty Rectangle Examples

Although it may seem like this advanced technique has several steps, identifying one and using it for eliminations is pretty simple.

Solving tip: If finding an empty rectangle is too tedious, you can look for a conjugate pair first. Sometimes those are easier to spot.

Empty Rectangle: L Shape

Empty rectangle patterns with L shapes have five cells that fall into exactly one row and one column in a single block, creating an L. The Ls can be in any direction. To find one and make eliminations follow these steps:

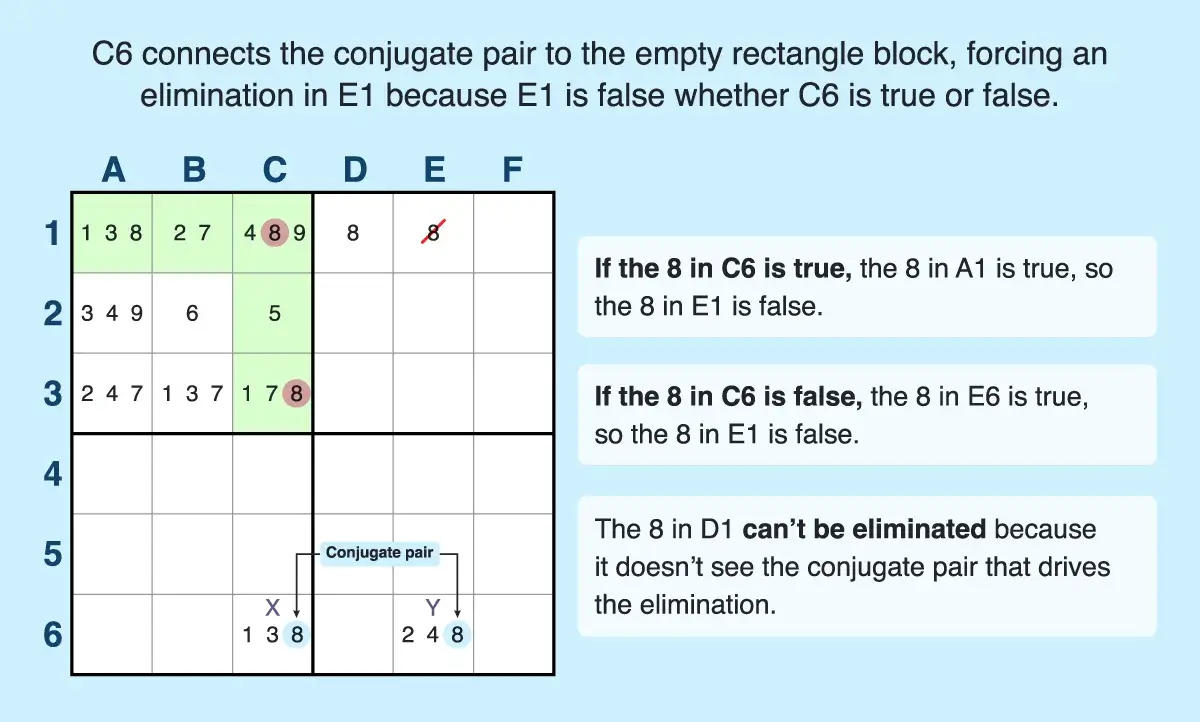
1. Find an empty rectangle. For example, five cells in the top-left block (A1, B1, C1, C2, and C3) form an L shape with candidate 8, using just one row and one column of the block. The four other cells outside of the row and column in that block do not contain that candidate number, forming an empty rectangle.
2. Find a conjugate pair with the same candidate number used in the L-shaped pattern. The conjugate pair must be in two different blocks and one cell must align with at least one cell of the L-shaped pattern, which contains the target digit. For example, row 6 has a conjugate pair of 8s in C6 and E6. This pair of cells are in two different blocks, and C6 aligns with the column cells of the empty rectangle pattern (C1 and C3) that contain the target number (8).
3. Make eliminations. The cell of the conjugate pair that shares a candidate with the L-shape's column (C6) is x and the cell that doesn't share a unit with the pattern (E6) is y. The elimination occurs in a cell that shares the row with the shape and the column with y, so you can eliminate the 8 in E1. But you can't eliminate the 8 in D1 because it doesn't share the column with y.

Empty Rectangle: T Shape

Empty rectangle patterns with T shapes have five cells that fall into exactly one row and one column in a single block, creating a T. Like the Ls, the T shapes can be in any direction. To find one and make eliminations follow these steps:

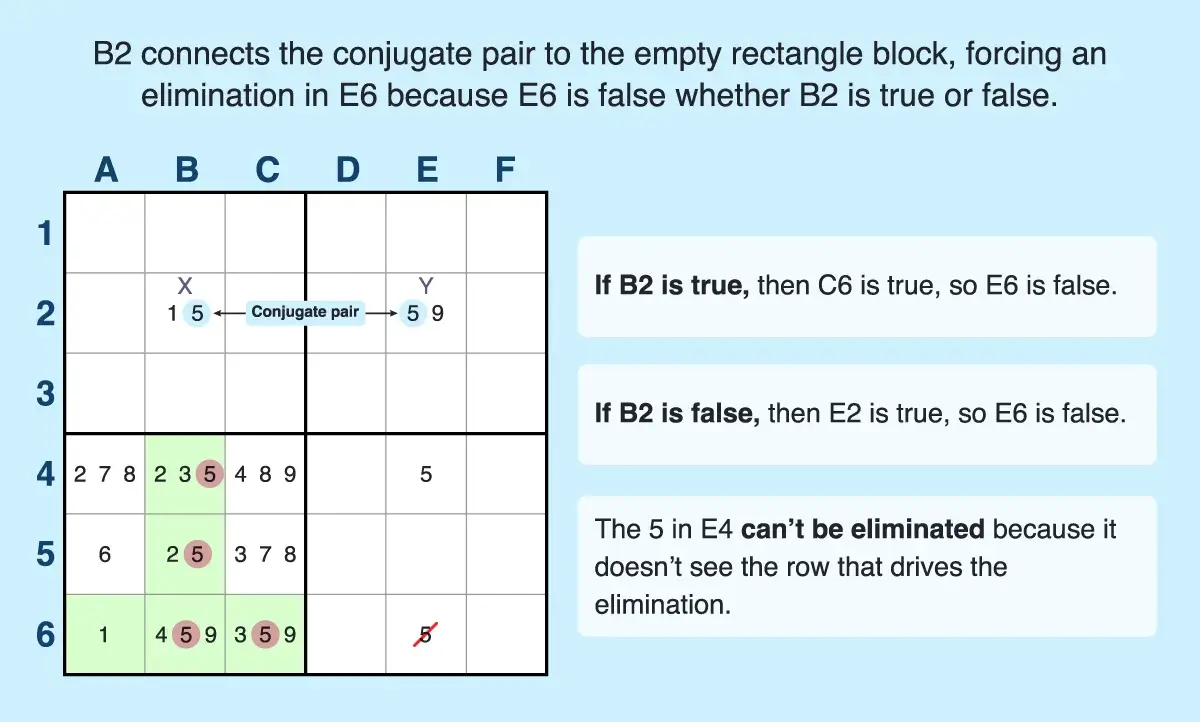
1. Find an empty rectangle. For example, five cells (B4, B5, B6, A6, and C6) form a T shape with candidate 5, and they fall into exactly one row and one column. The four cells of the block outside of that row and column do not contain that candidate number, forming the empty rectangle.
2. Find a conjugate pair with the same candidate number used in the T-shaped pattern. The conjugate pair must be in two different blocks and one cell must align with at least one cell of the T-shaped pattern. For example, row 2 has a conjugate pair of 5s in B2 and E2. This pair of cells are in two different blocks, and B2 aligns with the column cells (B4, B5, and B6) of the pattern, which also contain the target number (5).
3. Make eliminations. The cell of the conjugate pair that shares a candidate with the T-shape's column (B2) is x and the cell that doesn't share a unit with the pattern (E2) is y. The elimination occurs in a cell that shares the row with the shape and the column with y, so you can eliminate the 5 in E6. But you can't eliminate the 5 in E4 because it doesn't share the column with y.

Empty Rectangle: Plus-Sign Shape

Empty rectangle patterns with plus-sign shapes have five cells that fall into exactly one row and one column in a single block, creating a plus sign with the four corners of the block outside of the shape. Because of their shape, plus signs can only be in one orientation. To find one and make eliminations follow these steps:

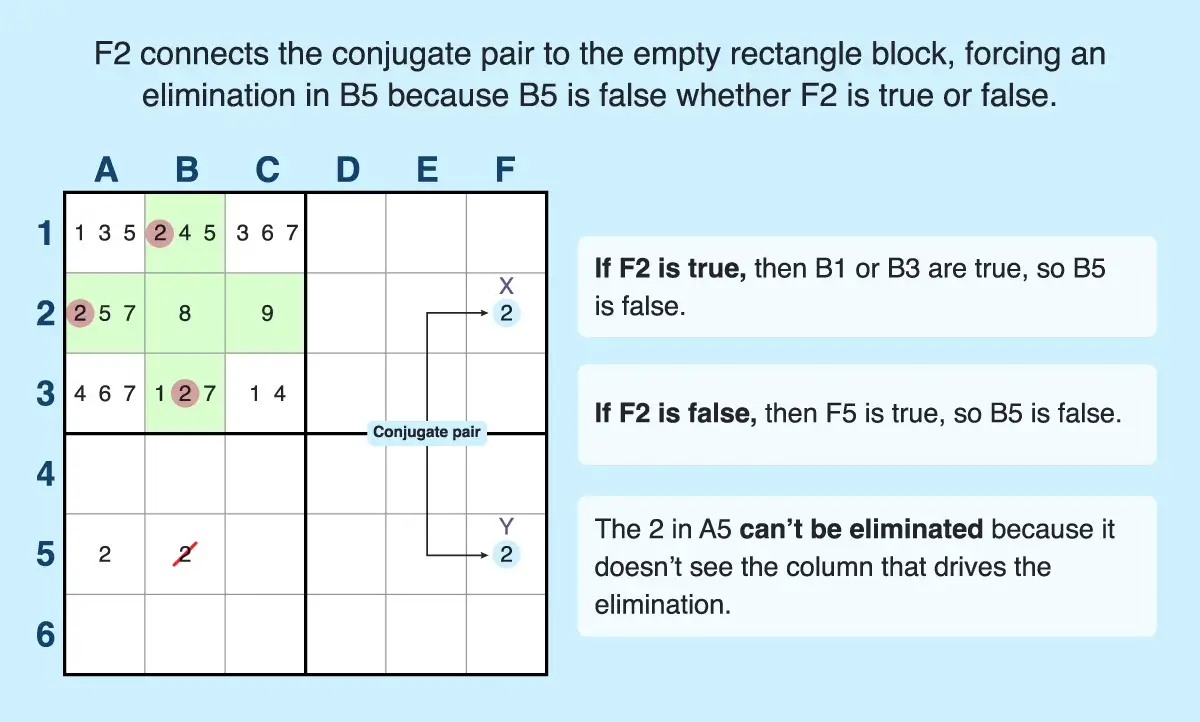
1. Find an empty rectangle. For example, five cells (B1, B2, B3, A2, and C2) form a plus-sign shape with candidate 2 and fall into exactly one row and one column. The four cells of the block outside of that row and column do not contain that candidate number, forming the empty rectangle.
2. Find a conjugate pair with the same candidate number as the plus-sign pattern. The conjugate pair must be in two different blocks and one cell must align with at least one cell of the plus-sign pattern. For example, column F has a conjugate pair of 2s in F2 and F5. This pair of cells are in two different blocks, and F2 aligns with the row cell (A2) of the pattern, which also contains the target number (2).
3. Make eliminations. The cell of the conjugate pair that shares a candidate with the plus-sign row (F2) is x and the cell that doesn't share a unit with the pattern (F5) is y. The elimination occurs in a cell that shares a column with the shape and a row with y, so you can eliminate the 2 in B5. But you can't eliminate the 2 in A5 because it doesn't share the complete column or row with the plus sign even though it shares the row with y.

Seasoned solvers and advanced beginners want to add the empty rectangle strategy to their system of solving, especially when tackling difficult puzzles. Try this Sudoku solving technique to unlock hard puzzles the next time you're playing Sudoku online.